Zad. 1. Spośród 30 uczniów pewnej klasy 17 lubi chodzić do szkoły, 22 - słuchać muzyki, a 25 - jeździć na rowerze. Ilu najwięcej może być takich uczniów, którzy nie lubią przynajmniej jednej z tych czynności?
Zad. 2. Średni wiek sześciorga dzieci jest równy 13 lat i 5 miesięcy. Dołącza do nich siódme dziecko, podnosząc średni wiek o dwa miesiące. Ile lat i miesięcy ma siódme dziecko?
Zad. 3. Jaki jest obwód figury zwanej sfinksem przedstawionej na poniższym rysunku?
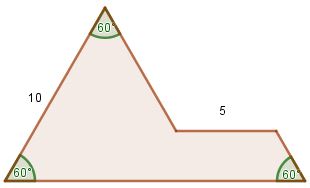
W kwietniu punkty zdobyli:
• 3 pkt. – Emilia Cichowska SP 14 Lubin, Paweł Michałowski SP 1 Białystok, Sandra Łuczak SP 107 Wrocław, Alicja Kaliszewska ZSP 1 Brzeg Dolny, Aleksandra Wiercińska SP Raszówka, Paulina Hołodniuk SP 2 Wołów, Piotr Musielak SP 3 Ścinawa, Igor Rączkiewicz SP Lewin Brzeski, Daria Dziedzic SP 107 Wrocław, Marta Goch SP 17 Wrocław, Grzegorz Kędzior SP 4 Warszawa, Justyna Kładoczna SP 118 Wrocław, Zuzanna Buraczewska SP 107 Wrocław, Szymon Grech Niepubliczna SP Koszarawa Bystra i Tymon Srokosz SP 52 Warszawa, Miłosz Zakrzewski SP Gostycyn;
• 2 pkt. – Jakub Malicki SP Kobierzyce, Alicja Szwarczyńska SP Kowalowa, Hanna Cicha OSM Wrocław, Marian Stawowy Salezjańska SP Wrocław, Antoni Adamus SP 4 Warszawa, Joanna Nowakowska SP 3 Głogów, Andrzej Nowak SP 2 Oborniki Śląskie, Oliwia Urbanek SP 6 Brzeg, Michał Sofiński SP 3 Syców, Dawid Stępień SP 15 Opole i Weronika Kiniorska SP 118 Wrocław;
• 1 pkt – Tymoteusz Noremberg SP 29 Wrocław, Amelia Gugała SP Wrzosów, Aleksander Porębny SP113 Wrocław, Anna Paszkiewicz SP 6 Świdnica i Mateusz Misztal SP 5 Kielce.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Spośród 30 uczniów 13 nie lubi chodzić do szkoły, 8 nie lubi słuchać muzyki i 5 nie lubi jeździć na rowerze. W takim razie tych, którzy nie lubią przynajmniej jednej z tych czynności, jest co najwyżej 13+8+5 = 26.
Zad. 2. Oznaczmy przez x wiek siódmego dziecka, wówczas 6.135/12 + x = 7.1319/12. Z rownania otrzymujemy x = 147/12. Sódme dziecko ma 14 lat i 7 miesięcy.
Zad. 3. Z definicji sfinksa jegi powierzchnia składa się z trójkata i równoległoboku, zatem x+y = 10 (patrz rysunek). Obwód figury wynosi 3.10 + 2.5 = 40.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
