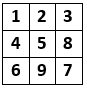
Zad. 1. W polach tabeli 3×3 rozmieść cyfry od 1 do 9 (każdą raz) tak, aby utworzyły kwadrat magiczny, tzn. aby sumy liczb w każdym wierszu, kolumnie i na obu przekątnych były takie same.
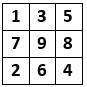
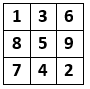
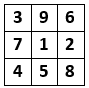
Zad. 2. W polach tabeli 3×3 rozmieść cyfry od 1 do 9 (każdą raz) tak, aby utworzyły kwadrat antymagiczny, tzn. aby sumy liczb w każdym wierszu, kolumnie i na obu przekątnych były za każdym razem inne.
Zad. 3. W polach tabeli 3×3 rozmieść cyfry od 1 do 9 (każdą raz) tak, aby utworzyły kwadrat, w którym liczba trzycyfrowa w drugim wierszu jest 2 razy większa, a liczba w trzecim wierszu jest 3 razy większa od liczby w pierwszym wierszu.
Wyniki:
W tym miesiącu punkty zdobyli:
- 3 pkt. - Weronika Buchar - nauczycielka matematyki z Leszna, Daria Bumażnik - doktorantka na Wydziale Chemii UWr, Agata Centkowska - informatyk z Biela, Wiktor Gatner SP 3 Wrocław, Elżbieta Grzechnik - emerytowana nauczycielka matematyki z Radomia, Dominika Horodecka - studentka WIMiO na Politechnice Gdańskiej, Vladislav Klyachin - programista z Berlina, Agata Leśnicka - lekarz z Gdańska, Krystyna Lisiowska - redaktor z Warszawy, Oliwia Makuch - studentka matematyki na PWr, Hanna Marcinowska LO 3 Opole, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Szymon Meyer - analityk danych z Dziewkowic, Joanna Miłkowska - pracownik biurowy ze Stalowej Woli, Wojciech Mura - student matematyki na UJ, Anna Niżałowska I LO Góra, Edward Nowicki - informatyk z Poznania, Kasper Przenzak - analityk ryzyka z Krakowa, Cezary Rębiś ZS Elektronicznych Radom, Rozalia Roguska - nauczycielka matematyki z Mierzęcina, Olga Shut - programistka z Wrocławia, Adam Stanisławski - programista z Wrocławia, Igor Sudyka V LO Kraków, Marzena Wąsiewicz - nauczycielka matematyki z Kajetan, Michał Węgrzyn - student UWr,
- 2 pkt. - Ignacy Włodarski SP 36 Wrocław.
Odpowiedzi:
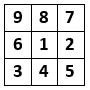
Zad. 1. Jedyną możliwość (z dokładnością do permutacji wierszy lub kolumn) przedstawia diagram poniżej.
Zad. 2. Kilka z wielu możliwości przedstawiają diagramy poniżej.
Zad. 3. Istnieją cztery kwadraty spełniające warunki zadania.
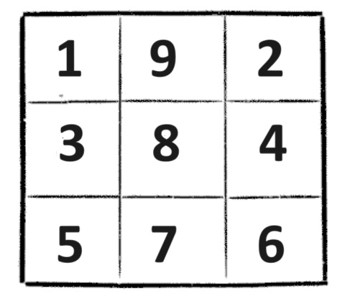384 = 2∙192, 576 = 3∙192
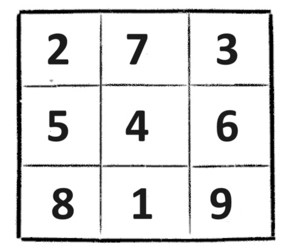
438 = 2∙219, 657 = 3∙219
546 = 2∙273, 819 = 3∙273
654 = 2∙327, 981 = 3∙327
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
