Pomóż Mikołajowi zapakować prezenty elegancko, a przy tym jak najbardziej ekonomicznie. Za każdym razem wybierz taki sposób zapakowania zabawki, który wymaga mniejszego pudełka. Określ, jakie wymiary będą potrzebne w tym zadaniu.
Odlotowe figury
Pakujemy prezenty... ekonomicznie
Kopalnia metod
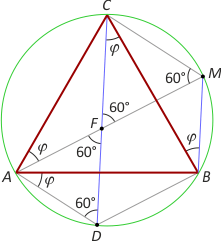Trójkąt równoboczny ABC wpisano w okrąg, a następnie na łuku BC obrano dowolny punkt M. Okazuje się, że |MA| = |MB| + |MC|. Ten zaskakujący fakt wykażemy na kilkanaście sposobów. Niektóre dowody opierają się na podobnym pomyśle, więc są prezentowane pod wspólnym tytułem.
Kosmiczny wzór na pole trójkąta
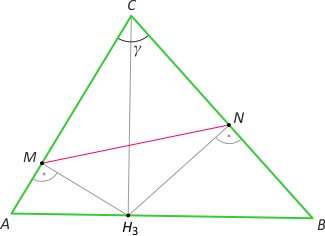Każdy licealista zna co najmniej kilka wzorów na pole trójkąta. A czy znacie taki wzór S = R·pH, gdzie R jest promieniem okręgu opisanego na trójkącie, a pH - połową obwodu trójkąta spodkowego? Kosmos... Trójkąt spodkowy trójkąta ostrokątnego ABC to taki trójkąt wpisany w trójkąt ABC, którego wierzchołkami są spodki wysokości trójkąta ABC. W artykule przeprowadzimy aż 10 dowodów wyżej wspomnianego wzoru, a przy okazji poznamy kilka innych interesujących faktów.
Piramida Sierpińskiego
Przygotujemy bryłę, która może być prawdziwą ozdobą gabinetu matematycznego. Pojedyncze elementy wykonuje się łatwo i szybko. Ponieważ całość ma budowę modułową, a do jej wykonania potrzebnych jest dużo elementów (co najmniej 64), może być wspólnym dziełem większej grupy uczniów.
Z siatki sześcianu
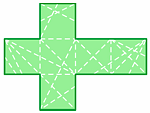Rysunek obok kojarzy z siatką sześcianu (jedną z 11 możliwych). A czy można z tej siatki skleić jeszcze jakiś inny wielościan? Jeśli umówimy się, że wielościan wolno rozcinać do siatki nie tylko wzdłuż krawędzi, ale także wzdłuż odcinków biegnących wewnątrz ścian, to z takiej siatki możemy posklejać kilka innych brył.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
