W artykule popatrzymy na bałwana z przymrużeniem oka.
Najprostszy model bałwanka tworzą trzy kule o jednakowych promieniach r = 0,2 m.
Wszystko widać. O czym tu jeszcze pisać? A jednak jest o czym.
Popatrz!
Nikt nie widzi bałwanka tak, jak na powyższym rysunku.
Bałwanek wygląda przecież tak:
albo tak:
To zależy, kto na niego patrzy: dorosły, czy dziecko. Nieprawdaż?
Trzy styczne kule pokazane na pierwszym rysunku
nie są widoczne w ten sposób z żadnego miejsca (na świecie!).
Zawsze choć jedna z nich wygląda tak, jakby nachodziła na sąsiednią.
Również i te ostatnie rysunki są nieco zakłamane.
Jeśli patrzymy na bałwanka z przymrużeniem oka (tzn. jednym okiem), to kule nie wyglądają na równe.
Popatrz!
Kula wydaje się większa, gdy kąt, pod jakim ją widzimy, jest większy.
Uwaga. Rozpatrujemy tu tylko aspekt czysto geometryczny. Człowiek patrzy okiem, a widzi mózgiem. Na rzeczywisty obraz nakładają się nasze wyobrażenia, doświadczenia, itp. W efekcie rozpoznajemy wielkości nie tylko na podstawie samego kąta widzenia.
Możesz zmieniać wielkości z, r i H,
przesuwając (ikona 
)
odpowiednie kropki wzdłuż odcinków).
Warto sprawdzić, jak wygląda bałwanek z odległości z = 1 m, a jak z wysokości H = 1,6 m itd.
Jak zmieniają się kąty widzenia?
(Dla znających trygonometrię: Jak obliczyć te kąty? Szczegóły znajdziesz, klikając
. )
Z daleka widać więcej?
Tak, to nie jest paradoks. Z większej odległości widać większą część powierzchni kuli.
Oczywiście jednym okiem widać zawsze mniej niż połowę jej powierzchni. Z dużej odległości widać prawie 50 % powierzchni. Jak to obliczyć dokładnie? Jaką część powierzchni Księżyca
widzimy z Ziemi? Czy to więcej niż 49 %?
Jak obliczyć, jaką część powierzchni kuli o promieniu r widać z odległości d (od środka kuli)?
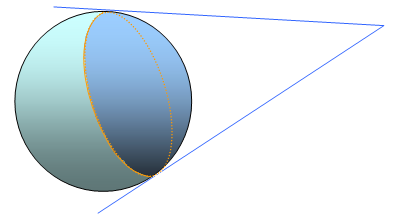
Do tego nie trzeba trygonometrii. Wystarczy piękne twierdzenie Archimedesa, które podamy tu bez dowodu:
Twierdzenie 1. Kulę o promieniu r zapakujmy do puszki o wysokości 2r i promieniu podstawy r.
Dwie płaszczyzny równoległe do podstaw puszki wycinają z powierzchni kuli obszar o takim samym polu, jak obszar wycięty przez te płaszczyzny z powierzchni bocznej puszki.
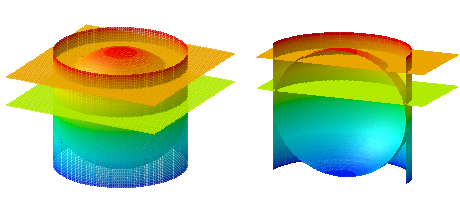
W szczególności, gdy te dwie płaszczyzny są płaszczyznami zawierającymi podstawy puszki, to pole powierzchni kuli jest równe polu powierzchni bocznej puszki. (Powierzchnia boczna puszki, po rozcięciu i rozprostowaniu, jest prostokątem o
wymiarach 2
r × 2r.)
Zatem mamy:
Wniosek 1. Pole powierzchni kuli o promieniu r jest równe
4r 2.
Ćwiczenie 1. Który równoleżnik wyznacza wokół bieguna obszar równy 1/4 powierzchni Ziemi?
Wskazówka 1.
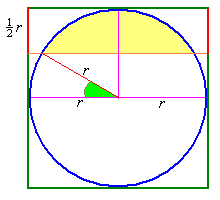
Wskazówka 2.
Odp.: 30o.
Wniosek 2. Gdy patrzymy na kulę o promieniu r z odległości d (mierzonej od środka kuli), to widzimy obszar o polu 1/2 - r/(2d) powierzchni całej kuli.
Uzasadnienie powyższego wniosku nie jest trudne. Przedstawione jest na poniższym rysunku.
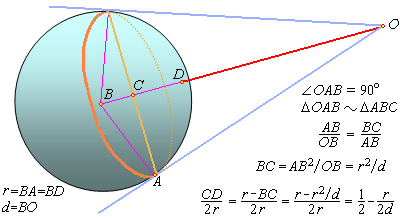
Na deser proponujemy kilka ćwiczeń (z kalkulatorem):
|
odległość Księżyc - Ziemia: |
Ćwiczenie 2. Satelity geostacjonarne 'wiszą nieruchomo' 35 tys. km nad równikiem (tzn. nad powierzchnią Ziemi). Ile z nich widać? (tzn. jaka część powierzchni Ziemi jest widoczna?)
Ćwiczenie 3. Czy z Ziemi widać więcej niż 49 % powierzchni Księżyca?
Ćwiczenie 4. Jaką część powierzchni Ziemi widać z Księżyca?
Ćwiczenie 5. Czy z samolotu lecącego na pułapie 10 km widać więcej niż 1 % powierzchni Ziemi?
Ćwiczenie 6. Jaki jest promień Słońca?
Wskazówka: W czasie zaćmienia Słońca tarcza Księżyca wygląda na równą tarczy Słońca.
Ćwiczenie 7* (z trygonometrią). Pod jakim kątem widzimy Księżyc z Ziemi?
Uwaga. Rachunki warto przeprowadzić dwukrotnie, wybierając skrajne dane (szczególnie w ćw. 4). Wtedy więcej widać - widać 'czułość' odpowiedzi na dane wejściowe.
Ćwiczenie 8. Z jakiej odległości widać (dokładnie) 1/3 powierzchni kuli o promieniu r ?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
