Kamienie domina mają grubość g = 0,7 cm,
szerokość s = 2 cm i wysokość w = 4 cm.
Ustawiamy je równo, jeden za drugim, w szeregu, co d = 2,5 cm
(to znaczy luka pomiędzy sąsiednimi kamieniami ma szerokość g - d = 1,8 cm).
Tak stoją.
|
Teraz lekko popychamy pierwszy kamień i... katastrofa!
Przewróciły się i... leżą. Ale jak leżą?
Leżą równo, oparte jeden na drugim,
tylko ostatni leży płasko.
A dokładniej jak leżą? Jak równo?
Zbadajmy to.
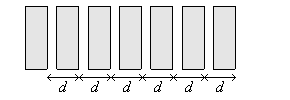Trzeba popatrzeć z boku.
(Rysujemy schematycznie, nie dbając o wymiary, tak, by wyraźniej pokazać problem).
Najpierw stoją równo.
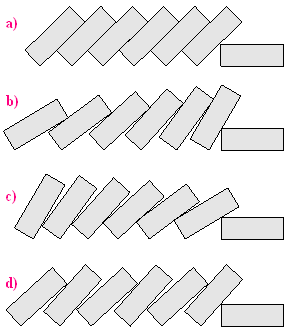
Potem leżą. Ale jak leżą?
Czy (z wyjątkiem ostatniego) leżą:
a) - 'równolegle',
b) - 'wygięte w dół',
c) - 'wygięte w górę',
d) - 'wygięte na przemian'?
Który rysunek jest najlepszy,
najwierniej oddaje rzeczywistość?
Właśnie ten problem przedyskutujemy w dalszej części artykułu.
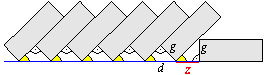Rysunek a) NIE JEST POPRAWNY!
Bowiem:
- wszystkie zaznaczone trójkąty są prostokątne,
- wszystkie zaznaczone żółte kąty są równe,
- wszystkie boki trójkątów leżące naprzeciw żółtych kątów
są równe g.
Zatem wszystkie zaznaczone trójkąty są przystające.
Zatem wszystkie przeciwprostokątne są równe d.
Zatem wszystkie przyprostokątne są KRÓTSZE od d.
Zatem z < d, a przecież kamienie stały w RÓWNYCH odstępach,
więc powinno być z = d .
Ta sprzeczność dowodzi, że rysunek a) jest niepoprawny.
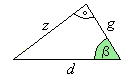Umowa.
W trójkącie prostokątnym o przeciwprostokątnej d i przyprostokątnej g oznaczmy:
przez z drugą przyprostokątną oraz przez
kąt pomiędzy g i d.
Uwaga. Odnotujmy, że gdyby ustawić kamienie w równych odstępach d
z wyjątkiem ostatniego, który ustawimy w odległości z,
to po upadku leżałyby one jak na rysunku a).
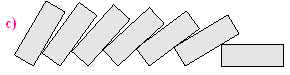
Dalej pokażemy, że najbliższy rzeczywistości
jest rysunek c),
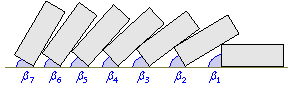że kąty
1,
2,
3,...
są większe od kąta :
1 >
,
2 >
,
3 >
,...
i ponadto, że te kąty są coraz mniejsze:
90o =
1 >
2 >
3 >...
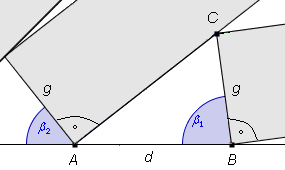
Przyjrzymy się dokładnie kątowi 2
i pokażemy precyzyjnie, że:
2 >
i
1 >
2 ,
przy czym nie będziemy korzystać z faktu,
że
1 = 90o;
wystarczy nam, że
1 >
(dlatego na rysunkach przedstawiamy
1
jako kąt ostry - to się później przyda).
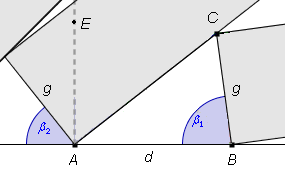
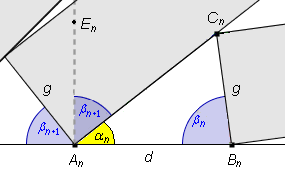
Po narysowaniu 'przerywanej' półprostej AE prostopadłej do AB widać jeszcze jeden kąt o mierze
2.
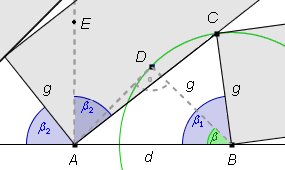Narysujmy okrąg o środku B i promieniu g.
Niech D będzie takim punktem okręgu,
że odcinek AD jest styczny do tego okręgu.
Wtedy trójkąt ABD to nasz 'znajomy' trójkąt o jednym z kątów równym
.
Na rysunku można dostrzec jeszcze jeden kąt o mierze
.
Zatem widać, że
2 >
.
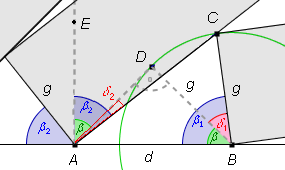By porównać kąty
1 =
+
1
i
2 =
+2,
wystarczy porównać kąty
1 i
2.
Mianowicie:
- w trójkącie równoramiennym CBD :
BDC =
(180o - 1)
=
90o
-
1 ,
- w trójkącie CAD :
2
=
180o -
ADC -
ACD =
=
180o -
(90o + 90o
-
1) -
ACD =
=
1 -
ACD
<
<
1.
Zatem uzasadniliśmy, że
2 >
i
1 >
2 .
Takie samo rozumowanie zastosowane do kolejnych trójkątów pokazuje, że:
3 >
i
2 >
3 ,
4 >
i
3 >
4 ,
5 >
i
4 >
5
i tak dalej.
Czyli zachodzą wszystkie poniższe nierówności:
1 >
2 >
3 > ...
.
Pokazaliśmy nawet trochę więcej - nie tylko to, że te kąty maleją i są większe od ,
ale także, że różnice:
1 -
=
1,
2 -
=
2,
3 -
=
3,
4 -
=
4,
. . .
są coraz mniejsze (coraz bliższe zera).
Tak jest, bo każda następna jest mniejsza od połowy poprzedniej.
(k+1
<
k).
Oznacza to, że kąty
1,
2,
3,...
są coraz bliższe kątowi
,
że coraz lepiej przybliżają
.
(W matematyce wyższej mówi się, że tworzą ciąg zbieżny do
.)
n+1
w zależności od
n .
Mianowicie:
mamy ostatecznie
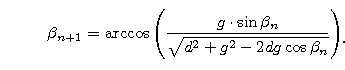
Za pomocą arkusza kalkulacyjnego można zobaczyć, jakie są to kąty
(można zmieniać pola z wartościami d i g) :
|
d = g = |
d = g = |
d = g = |
|
|
1 |
90o | 90o | 90o |
|
2 |
o | o | o |
|
3 |
o | o | o |
|
4 |
o | o | o |
|
5 |
o | o | o |
|
6 |
o | o | o |
|
7 |
o | o | o |
|
8 |
o | o | o |
|
9 |
o | o | o |
|
. . . |
. . . |
. . . |
. . . |
Te liczby wyraźnie pokazują, że kąty
n
bardzo szybko zbliżają się do granicznej wartości
.
Arkusz kalkulacyjny 'oszukuje', podając identyczne kąty pod koniec kolumn. To jest błąd zaokrągleń. Te kąty są 'niemal równe'.
Oznacza to, że kamienie domina leżą 'niemal równolegle'.
(Trzeba pisać 'niemal', bo wiemy przecież, że zawsze jest pomiędzy nimi nierówność.)
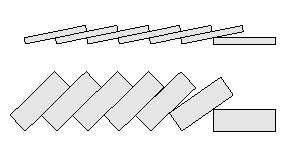
A zatem jak naprawdę leżą kamienie domina?
Tak, jak na rysunku obok -
'niemal równolegle',
choć oglądane pod lupą są 'wygięte do góry'.
Leżą tym bardziej płasko, im większy jest stosunek d : g.
