h-Ekierki

Jak wyglądają ekierki?
Zobacz.

 

 

Ekierka to po prostu trójkąt z wyciętym mniejszym trójkątem,
przy czym ten wewnętrzny trójkąt ma boki w jednakowej odległości od boków zewnętrznego.

Będziemy mówić, że h-ekierka ABC ma otwór A'B'C',
gdy boki A'B', B'C', A'C' są w odległości h od boków AB, BC, AC.

Przeczytaj poniższe zadanie.

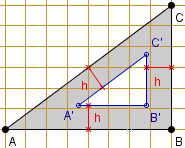ZADANIE 0.   
Boki h-ekierki ABC mają długości: AB = 8, BC = 6, AC = 10.
 
  a)  Oblicz pole i obwód otworu A'B'C', gdy h = 1.
 
  b)  Oblicz pole i obwód otworu A'B'C', gdy h = 0,5.
 
  c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
 
  d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

Omówimy pewien pomysł rozwiązania tego zadania.

Widać, że

trójkąty ABC i A'B'C' są podobne.
Tak jest, bo boki trójkąta A'B'C' są równoległe do boków trójkąta ABC, zatem trójkąty te mają jednakowe kąty, a więc (z cechy kkk) są podobne.

Kluczem do rozwiązania jest znalezienie skali podobieństwa s tych trójkątów.
Zobacz.

 

 

Powyższy rysunek wyjaśnia, że

trójkąty A'B'C' i ABC są jednokładne
względem środka O okręgu wpisanego w trójkąt ABC,
w skali s = (r - h)/r, gdzie r oznacza promień tego okręgu.
Przyjrzyj się n.p. odcinkom A'B' i AB. Jaki jest stosunek ich długości?

Aby rozwiązać zadanie 0, wystarczy jeszcze znaleźć promień r okręgu wpisanego w ABC.
Łatwo go obliczyć z zależności

1/2 × promień okręgu wpisanego × obwód = pole.

 

Tak samo można rozwiązać poniższe modyfikacje Zadania 0.

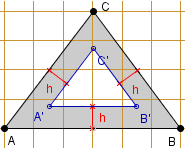ZADANIE 1.   
Boki h-ekierki ABC mają długości: AB = 6, BC = 5, AC = 5.
a)  Oblicz pole i obwód otworu A'B'C', gdy h = 1.
b)  Oblicz pole i obwód otworu A'B'C', gdy h = 0,5.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

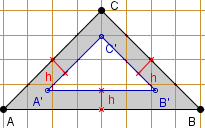ZADANIE 2.   
Boki h-ekierki ABC mają długości: AB = 8, BC = 5, AC = 5.
a)  Oblicz pole i obwód otworu A'B'C', gdy h = 1.
b)  Oblicz pole i obwód otworu A'B'C', gdy h = 0,5.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

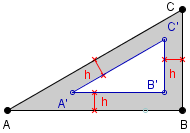ZADANIE 3*.   
Boki h-ekierki ABC mają długości: 10, 10, 20.
a)  Oblicz pole i obwód otworu A'B'C', gdy h = 1.
b)  Oblicz pole i obwód otworu A'B'C', gdy h = 0,5.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

ZADANIE 4*.   
Boki h-ekierki ABC mają długości: a, b, c i tworzą trójkąt prostokątny o przeciwprostokątnej c.
a)  Wyznacz pole i obwód A'B'C' w zależności od a, b, c, h.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

Nudne?
Zobacz więc, co się dzieje przy h > r.

 

 

ZADANIE 5.   
Ile rozwiązań mają podpunkty b) i b) w zadaniach 1-4?
Czy mają jakieś rozwiązanie dla h > r?

 

ZADANIE 6.   
Znajdź największą wartość h, przy której trójkąt A'B'C' leży w obrębie trójkąta ABC:
 a)  w h-ekierce ABC, gdzie AB = 8, BC = 6, AC = 10,
 b)  w h-ekierce ABC, gdzie AB = 8, BC = 5, AC = 5,
 c)  w h-ekierce ABC, gdzie AB = 6, BC = 5, AC = 5,
 d)  w h-ekierce ABC, gdzie AB = 10, BC = 10, AC = 20,
 e*)  w prostokątnej h-ekierce ABC o przyprostokątnych a, b i przeciwprostokątnej c.

 

---

 

A dlaczego by nie rozważać czworokątnych ekierek?

Będziemy mówić, że h-ekierka ABCD ma otwór A'B'C'D',
gdy boki A'B', B'C', C'D', A'D' są w odległości h od boków AB, BC, CD, AD.

 

 

Jeśli w czworokątną h-ekierkę jest wpisany okrąg, to łatwo rozwiązać zadania podobne do tych dla trójkąta.Sprawdź.

ZADANIE 7.   
Rozważmy h-ekierkę ABCD będącą trapezem prostokątnym o podstawach długości 30, 15 i wysokości 20.
a)  Oblicz pole i obwód otworu A'B'C'D', gdy h = 1.
b)  Oblicz pole i obwód otworu A'B'C'D', gdy h = 0,5.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

 

Inaczej jest w poniższej h-ekierce.

ZADANIE 8.   
Rozważmy h-ekierkę ABCD będącą trapezem prostokątnym o podstawach długości 35, 20 i wysokości 20.
a)  Oblicz pole i obwód otworu A'B'C'D', gdy h = 1.
a')  Czy otwór A'B'C'D' jest podobny do ABCD, gdy h = 1?
b)  Oblicz pole i obwód otworu A'B'C'D', gdy h = 0,5.
b')  Czy otwór A'B'C'D' jest podobny do ABCD, gdy h = 0,5?
e)  Czy jest takie h, że otwór A'B'C'D' jest podobny do ABCD?

 

 

 

---

 

A dlaczego by nie rozważać dowolnych wielokątnych h-ekierek?

ZADANIE 9*.   
Wielokątna h-ekierka w z otworem w' jest opisana na okręgu o promieniu r, przy czym
w ma pole P_w i obwód OB_w.
a)  Wyznacz pole P_w' i obwód Ob_w' otworu w' w zależności od h.
c)  Dla jakiej wartości h pole otworu jest połową pola ekierki?
d)  Dla jakiej wartości h obwód otworu jest cztery razy mniejszy od obwodu ekierki?

 

 

ZADANIE 10**.   

Wielokątna h-ekierka w ma otwór w'.
Czy wielokąt w jest podobny do w' wtedy i tylko wtedy, gdy w w można wpisać okrąg?

 

---