K-kładki

O tym jak budować T-kładki z dwóch desek pisaliśmy już w artykule T-kładki.
Teraz omówimy różne sposoby budowania kładek z większej liczby desek.

Rzeka tworzy zakręt, a raczej rozlewisko, które kształtem przypomina kąt (o mierze ). Aby skrócić drogę, można przerzucić jedną deskę. To jest najprostsza K-kładka. Gdy mamy cztery jednakowe deski o długości d = 1,5m, można je ułożyć tak, że utworzą większy skrót, nową K-kładkę. (Przesuwając suwak >>>, zobaczysz kolejne etapy konstrukcji.)

 

 

Budujemy kładki bez gwoździ, 'na zakładkę'. Gdy mamy jeszcze trzy deski (tej samej długości d), kładziemy je na poprzednich, według tego samego schematu. Z dziesięciu desek można ułożyć jeszcze większy skrót. Dostawiając kolejne trójki desek, tworzymy następne K-kładki.

 

 

Czy możemy dowolną liczbę razy powtarzać tę konstrukcję?
Czy możemy dowolnie daleko (od Z) przeciąć dwusieczną kąta ?

To są DWA pytania.
Na pierwsze z nich odpowiedź brzmi TAK. Omówimy to na poniższym rysunku.

Ponieważ kąt ZZ₂A₃ > 90^o, kąt ZZ₃A₃ > 90^o (dlaczego?).
Zatem Z₂A₃ > Z₃A₃ (bo w trójkącie najdłuższy bok leży na przeciwko największego kąta).
Stąd d > Z₃A₃, więc okrąg o środku Z₃ i promieniu d, wyznaczający A₄, przetnie półprostą ZA₃ POZA odcinkiem ZA₃, czyli kąt ZZ₃A₄ też jest rozwarty.
I tak dalej. Za każdym razem dostajemy takie kąty, że można dostawiać następne deski. Nie ma przeszkód (geometrycznych), by poprawić K-kładkę, budując następną i tworząc jeszcze lepszy skrót.

 

 

Choć tę konstrukcję możemy powtarzać dowolną liczbę razy, nigdy nie osiągniemy punktu L dwusiecznej kąta , co wyjaśnia poniższy rysunek.

 

 

PRZESTROGA.   Obliczanie odległości ZZ₁, ZZ₂, ZZ₃,... jest trudne.
Nawet w przypadku = 90^o, d = 1 skomplikowany jest wzór rekurencyjny, określający zależność pomiędzy ZZ _{n + 1} a ZZ_n :
 

ZZ _{n + 1} = ZZ_n + ( 1 - ZZ_n² ) / ( 2 + 2 ZZ_n ( 2 - ZZ_n² ) ^1/2 ) .

 

---

 

Podamy teraz inny sposób budowania K-kładek. Może on pozwoli robić jeszcze lepsze skróty.
Oprócz jednakowych desek potrzebny będzie... parametr s - rolę, jaką odgrywa on w konstrukcji, zobaczysz na poniższym rysunku (zmieniaj położenie suwaka s  i zmieniaj bardzo powoli położenie suwaka >>>).

 

 

Jest to modyfikacja poprzedniej konstrukcji (s = 0,5).
Ma te same 'dobre' i 'złe' cechy co poprzednia:
- można kontynuować ją bez ograniczeń, osiągając coraz lepsze skróty,
- nie można osiągnąć punktu L (co ilustruje poniższy rysunek).

 

 

Punkt L - limit naszej konstrukcji - oddala się od Z, gdy s maleje.
W pierwszej chwili wydaje się, że najlepsze rezultaty da konstrukcja dla s prawie równego 0.
Co zauważasz, przesuwając suwak s?
Limit L oddala się, ale coraz trudniej do niego się zbliżyć, potrzeba coraz więcej desek.
 
Uwaga. Znam tylko bardzo trudne rachunkowo uzasadnienie, że L jest granicą ciągu Z_n.
Może ktoś z Czytelników znajdzie prosty dowód?

 

---

 

Ciągle nie wiemy, czy można podać konstrukcję K-kładek, osiągających dowolnie dalekie punkty dwusiecznej kąta . Na poniższym rysunku powtórzono cztery razy pomysł z pierwszej konstrukcji (przesuń suwak >>>, a zobaczysz nowe możliwości, nowy suwak).

 

 

Udaje się zatem przekraczać poprzednie limity. Jednak powyższy rysunek nie określa żadnej procedury, nie podaje algorytmu budowania K-kładek. Uzasadnia, że można poprawiać poprzednie wyniki, ale czy w ten sposób można zajść dowolnie daleko?

 

---

 

Poniższy schemat budowania A-kładek jest odmienny od poprzednich.

Omówimy go na przykładzie, przy wartości n = 6.
- Najpierw po obu stronach Z odkładamy pierwszą warstwę desek, po trzy z każdej strony.
- Na tej pierwszej warstwie kładziemy drugą tak, że deski tej warstwy łączą środki sąsiednich desek z poprzedniej warstwy. Kładziemy zatem 5 desek (środkową przycinamy).
- Na tej drugiej warstwie kładziemy trzecią tak, że deski tej warstwy łączą środki sąsiednich desek z poprzedniej warstwy. Kładziemy zatem 4 deski (dwie przycinamy).
- Na trzeciej warstwie kładziemy warstwę czwartą (złożoną z 3 desek) według tego samego schematu.
- Na czwartej - piątą (złożoną z 2 desek) według tego samego schematu.
- Na piątej - szóstą = ostatnią (złożoną z 1 deski) według tego samego schematu.

Ile desek zużyliśmy? Ile jest zbędnych? (Zbędne są te, które leżą w całości na brzegu.)

 

 

Na poniższym rysunku widać konstrukcję dla innych, parzystych wartości parametru n.

W konstrukcji A-kładki z parametrem n = 2m zużywa się m(2m+1) desek.
Wiele jest zbędnych. Odrzucając je, zużyjemy m ² desek.

 

 

Niech Z_n oznacza środek deski (jedynej) w ostatniej warstwie (czyli w warstwie n-tej) A-kładki zbudowanej dla parametru n = 2m. 
Można uzasadnić (metodami matematyki wyższej), że dla dużych wartości parametru m, mamy

Oznacza to, że takie A-kładki mogą osiągnąć dowolnie dalekie punkty dwusiecznej kąta .
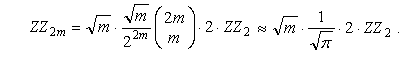
Co więcej, jeśli mamy punkt dwusiecznej w pewnej A-kładce, oddalony od Z o k ^. ZZ₂ , to minimalna liczba desek tej A-kładki jest rzędu  k ⁴ (to znaczy, że liczba desek jest w przybliżeniu proporcjonalna do  k ⁴). 

Powyższe A-kładki dają pewien algorytm budowania skrótów.
Naturalne jest pytanie, czy można znaleźć lepszy sposób.

A jeśli podamy inny sposób, to jak zmierzyć, czy on jest rzeczywiście lepszy?
Ekonomiści wiedzą jak - lepszy znaczy tańszy. W tym przypadku można powiedzieć, że lepszy znaczy mniejszego rzędu.

Problem znalezienia najlepszej (najtańszej) konstrukcji skrótów, wygląda na trudny. Być może nie można go w ogóle rozwiązać.
Można jednak oszacować koszty skrótów. Na przykład nietrudno jest uzasadnić, że każdy schemat budowania skrótów musi być co najmniej rzędu  k ². Zatem każdy algorytm tego rzędu, można uznać za prawie najlepszy - wystarczy go odgadnąć!

---

 

Na koniec pokażemy, skąd wziął się pomysł konstrukcji A-kładek. Widać to na rysunku.

 

 

---