| więcej informacji o tekście: |
W sześcianie o krawędzi AB = a będziemy rozważać kolekcje pewnych wielokątów. Podamy tylko lakoniczne opisy tych kolekcji. Mamy nadzieję, że rysunki 'mówią same za siebie'. Odpowiedzi do części zadań można zobaczyć(!). Wystarczy odpowiednio obrócić sześcian. Spróbuj.
Kolekcja I
Dla ustalonej wartości parametru x kolekcję tworzy 13 wielokątów:
- kwadrat o boku PQ = x, 'centralnie' położony w połowie wysokości (o bokach równoległych do boków podstawy),
- 4 trójkąty zaczepione na pionowych krawędziach - nazwijmy je skrzydełkami,
- 8 trapezów.
Dzięki sterom 3D wielokąty w sześcianie można oglądać z różnych stron.
Górne są przezroczyste, by nie zasłaniały reszty. Można je uczynić niewidocznymi.
Włączając [układ], można przesuwać sześcian, chwytając za początek układu współrzędnych.
Zadanie I.1. W tej kolekcji, jeśli x zmienia się od 0 do a = 6, to:
a)
pole jednego skrzydełka APA' zmienia się od . . . . . . . do . . . . . . . ,
b)
długość AP zmienia się od . . . . . . . do . . . . . . . ,
c)
kąt nachylenia trapezu APQB do podstawy zmienia się od . . . . . . . do . . . . . . . ,
d)
kąt pomiędzy trapezami o wspólnym boku PQ zmienia się od . . . . . . . do . . . . . . . ,
e*)
pole trapezu APQB zmienia się od . . . . . . . do . . . . . . . ,
f*)
kąt pomiędzy trapezami o wspólnym boku AP zmienia się od . . . . . . . do . . . . . . . .
Zadanie I.2. Oblicz łączne pole wielokątów tej kolekcji, gdy:
a)
a = 6, x = a/2 = 3,
b)
a = 6, x = 4,
c)
a = 6, x = 1.
Zadanie I.3. a = 6.
a)
Czy w tej kolekcji skrzydełka mogą być trójkątami równobocznymi?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
b)
Czy w tej kolekcji skrzydełka mogą być trójkątami prostokątnymi (równoramiennymi)?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
c*)
Czy w tej kolekcji trapezy mogą mieć ramiona tej samej długości, co krótsza podstawa?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
d)
Czy w tej kolekcji suma pól skrzydełek (trójkątów) może być równa sumie pól trapezów?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
Kolekcja II
Dla ustalonej wartości parametru y kolekcję tworzy 12 wielokątów:
- 4 skrzydełka - trapezy równoramienne o krótszej podstawie równej 2y ,
- 8 trójkątów.
Zadanie II.1. W tej kolekcji, jeśli y zmienia się od 0 do a/2 = 3, to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
kąt nachylenia trójkąta AKB do podstawy zmienia się od . . . . . . . do . . . . . . . ,
c)
pole trójkąta AKB zmienia się od . . . . . . . do . . . . . . . ,
d)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . ,
e)
kąt pomiędzy trójkątami AKB i CKD zmienia się od . . . . . . . do . . . . . . . ,
f)
kąt pomiędzy trójkątami AKB i BKC zmienia się od . . . . . . . do . . . . . . . ,
g)
kąt pomiędzy skrzydełkiem o boku AK i trójkątem AKB zmienia się od . . . . . . . do . . . . . . . .
Zadanie II.2. Oblicz łączne pole wielokątów tej kolekcji, gdy:
a)
a = 6, y = a/4 = 1,5,
b)
a = 6, y = 2,
c)
a = 6, y = 1.
Zadanie II.3. a = 6.
a)
Czy w tej kolekcji trójkąty mogą być trójkątami równobocznymi?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
b)
Czy w tej kolekcji trójkąty mogą być trójkątami prostokątnymi (równoramiennymi)?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
c*)
Czy w tej kolekcji trapezy mogą mieć ramiona tej samej długości, co krótsza podstawa?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
d*)
Czy w tej kolekcji suma pól skrzydełek (trapezów) może być równa sumie pól trójkątów?
Jeśli tak, to jakie jest wtedy łączne pole wielokątów?
Kolekcja III
Dla ustalonych wartości parametrów x i y kolekcję tworzy 21 wielokątów:
- kwadrat o boku PQ = x, 'centralnie' położony w połowie wysokości (o bokach równoległych do boków podstawy),
- 4 skrzydełka - trapezy równoramienne o krótszej podstawie długości 2y ,
- 12 trapezów przy dolnej i górnej podstawie sześcianu,
- 8 prostokątów o wymiarach x × y okalających brzeg kwadratu.
Zadanie III.1ax. W tej kolekcji, przy ustalonym a i x, jeśli y zmienia się od 0 do a/2 , to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . ,
c)
pole trapezu o podstawie AB zmienia się od . . . . . . . do . . . . . . . ,
Zadanie III.1ay. W tej kolekcji, przy ustalonym a i y, jeśli x zmienia się od 0 do a/2 , to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . ,
c)
pole trapezu o podstawie AB zmienia się od . . . . . . . do . . . . . . . .
Zadanie III.2. Oblicz łączne pole wielokątów tej kolekcji, gdy:
a)
a = 6, x = a/2, y = a/4,
b)
a = 6, x = y = a/4,
c)
a = 6, x = a/6, y = a/3.
Zadanie III.3. Oblicz łączne pole wielokątów tej kolekcji w zależności od parametrów a, x oraz y.
Zadanie III.4*. a = 6.
a)
Czy w tej kolekcji wszystkie 12 trapezów może mieć jednakowe krótsze podstawy?
Jeśli tak, to dla jakich wartości x i y?
b)
Czy w tej kolekcji wszystkie 12 trapezów może mieć jednakowe wysokości?
Jeśli tak, to dla jakich wartości x i y?
c)
Czy w tej kolekcji może być tak, że wszystkie trapezy są jednakowe (przystające)?
Jeśli tak, to dla jakich wartości x i y?
d)
Czy w tej kolekcji może być tak, że każdy trapez jest połową sześciokąta foremnego?
Jeśli tak, to dla jakich wartości x i y?
e)
Czy w tej kolekcji może być tak, że w każdym trapezie ramiona są tej samej długości, co krótsza podstawa?
Jeśli tak, to dla jakich wartości x i y?
f)
Czy w tej kolekcji suma pól skrzydełek może być równa sumie pól pozostałych trapezów?
Jeśli tak, to dla jakich wartości x i y?
Kolekcja IV
Dla ustalonych wartości parametrów x i y kolekcję tworzy 21 wielokątów:
- kwadrat o boku PQ = x i środku O w środku sześcianu,
- 4 pięciokątne skrzydełka,
- 16 trójkątów (rysunek wyjaśnia szczegóły).
Zadanie IV.1ax. W tej kolekcji, przy ustalonym a i x, jeśli y zmienia się od 0 do a/2 , to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole trójkąta AKB zmienia się od . . . . . . . do . . . . . . . ,
c)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . .
Zadanie IV.1ay. W tej kolekcji, przy ustalonym a i y, jeśli x zmienia się od 0 do a/2 , to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole trójkąta AKB zmienia się od . . . . . . . do . . . . . . . ,
c)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . .
Zadanie IV.2. Oblicz łączne pole wielokątów tej kolekcji w zależności od parametrów a, x i y.
Zadanie IV.3*. a = 6.
a)
Czy w tej kolekcji trójkąt PQK może być równoboczny?
Jeśli tak, to dla jakich wartości x i y?
b)
Czy w tej kolekcji trójkąt PQK może być prostokątny (równoramienny)?
Jeśli tak, to dla jakich wartości x i y?
c)
Czy w tej kolekcji może być tak, że wszystkie 16 trójkątów jest jednakowych (przystających)?
Jeśli tak, to dla jakich wartości x i y?
d)
Czy w tej kolekcji może być tak, że wszystkie 16 trójkątów jest podobnych?
Jeśli tak, to dla jakich wartości x i y?
e)
Czy w tej kolekcji może być tak, że AK = KP?
Jeśli tak, to dla jakich wartości x i y?
f)
Czy w tej kolekcji suma pól skrzydełek może być równa sumie pól wszystkich trójkątów?
Jeśli tak, to dla jakich wartości x i y?
Kolekcja V
Dla ustalonych wartości parametrów x, y i z kolekcję tworzy 21 wielokątów:
- kwadrat o boku PQ = x,
- 4 pięciokątne skrzydełka,
- 16 trapezów.
Zadanie V.1axz. W tej kolekcji, przy ustalonym a, x i z, jeśli y zmienia się od 0 do a/2 , to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . .
Zadanie V.1ayz. W tej kolekcji, przy ustalonym a, y i z, jeśli x zmienia się od 0 do a, to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . .
Zadanie V.1axy. W tej kolekcji, przy ustalonym a, x i y, jeśli z zmienia się od 0 do . . . . . ., to:
a)
długość AK zmienia się od . . . . . . . do . . . . . . . ,
b)
pole jednego skrzydełka zmienia się od . . . . . . . do . . . . . . . .
Zadanie V.2. Podkolekcje tej kolekcji są nam już znane, w szczególności:
a)
gdy x = 0 i z = . . . . . . . ,
to otrzymujemy kolekcję II ,
b)
gdy . . . . . . . . . . . . . . . . . . ,
to otrzymujemy kolekcję IV,
c)
gdy . . . . . . . . . . . . . . . . . . ,
to otrzymujemy kolekcję III ,
d)
gdy . . . . . . . . . . . . . . . . . . ,
to otrzymujemy kolekcję I .
Zadanie V.3. Łączne pole skrzydełek jest iloczynem pewnej stałej i wyrażenia
(![]() /2az + ay - xy). Jaka to stała?
/2az + ay - xy). Jaka to stała?
Zadanie V.4. Sprawdź, że łączne pole wielokątów tej kolekcji w zależności od parametrów
a, x, y oraz z wyraża się wzorem
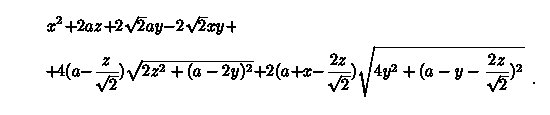
Zadanie V.5. W tej kolekcji punkt P leży na odcinku łączącym środek krawędzi AA' ze środkiem sześcianu, a punkt K leży 'pod' tym odcinkiem.
Tę samą kolekcję można opisać innymi parametrami. Niech:
- u oznacza odległość punktu P od krawędzi AA',
- v oznacza odległość punktu K od podstawy ABCD
- w oznacza odległość punktu K od ściany ABB'A'.
Podaj wzór opisujący łączne pole wielokątów tej kolekcji w zależności od wartości parametrów a, u, v oraz w.
Dalszy ciąg przygód kolekcji wielościanów w sześcianie znajdziesz tutaj.







