| Dynamiczne rysunki w tekście zrobiono w Geogebrze |
W artykule Środki par zbiorów można zobaczyć, jak tworzyć zbiór środkowy dla danych dwóch figur A i B, czyli zbiór środków odcinków łączących te figury. Leży on pomiędzy A i B. Tym razem utworzymy całą kolekcję zbiorów płynnie przechodzących od figury A do figury B, czyli tzw. odcinek figur.
Zapis (1 - t) . P + t . Q ma w tym tekście (jak i w matematyce wyższej) wiele znaczeń.
Określenie 1. Gdy P i Q są liczbami, a t jest ustaloną liczbą pomiędzy 0 i 1, to
Równość (1 - t) . P + t . Q = P + t . ( Q - P ) można bowiem zinterpretować następująco:
Określenie 2. Gdy P i Q są punktami płaszczyzny, a t jest ustaloną liczbą pomiędzy 0 i 1, to
Wtedy w układzie współrzędnych dla P(a, c), Q(b, d) i Z(x, y), mamy
y = (1 - t) . c + t . d .
Gdy t zmienia się od 0 do 1, to punkt (1 - t) . P + t . Q przebiega cały odcinek.
Ilustruje to poniższy rysunek (kliknij przycisk w lewym dolnym rogu).
Określenie 3. Gdy A i B są figurami płaskimi, a t jest ustaloną liczbą pomiędzy 0 i 1, to
Oczywiście:
dla t = 0, mamy (1 - 0) . A + 0 . B = A, bo 1.P + 0.Q = P i P przebiega całe A,
dla t = 1, mamy (1 - 1) . A + 1 . B = B, bo 0.P + 1.Q = Q i Q przebiega całe B,
dla t =
o czym pisaliśmy już w tekście Środki par zbiorów.
Na poniższym rysunku zobaczysz figury
(1 - t) . A + t . B
dla wypukłych wielokątów A i B.
Składają się ze zmniejszonych kopii figury A (w skali 1-t) i figury B (w skali t).
Określenie 3'. Gdy A i B są figurami płaskimi, to odcinkiem AB nazywamy kolekcję figur
Na poprzednim rysunku zobaczysz odcinki AB (tzn. kolekcje figur), gdy zmieniać będziesz t (kliknij przycisk w lewym dolnym rogu).
Trudniej jest zobaczyć odcinek
Choć A i B mają pole 0, to figury odcinka AB różne od końców, mają (zazwyczaj) pole > 0.
Niektóre z nich (dla pewnych t) są 'dziurawe', a inne nie. Ilustruje to poniższy rysunek.
Można zacząć od prostszych przykładów, jedną z łamanych zamieniając na odcinek.
Gdy A jest łamaną, a B jest kołem, odcinek AB, czyli kolekcja
Układając łamaną w kształt brzegu trójkąta lub prostokąta, zobaczysz, że odcinki AB wyglądają wtedy stosunkowo prosto.
Dla figur A i B odcinek AB, czyli kolekcja figur
To, o czym była tu mowa, może być przydatne przy tworzeniu... filmów animowanych.
Dawniej, by w takich filmach uzyskać wrażenie ruchu, tworzono kadry - wiele rysunków na każdą sekundę filmu. Na poszczególnych rysunkach stopniowo Lolek podnosił rękę albo Reksio merdał ogonem. Odcinek AB automatyzuje 'płynne przejście' od A - Bolka zdrowego, z kwadratową głową, do B - Bolka spuchniętego, z głową okrągłą (tylko nieco bardziej skomplikowanie niż na powyższym rysunku).
Teraz z łatwością robią to komputery. Nie tylko w filmach animowanych.
Można sobie wyobrażać, że tak może działać kompresja, czyli pakowanie filmu na dysk. Zapamiętuje się tylko niektóre fragmenty prawdziwego 24 klatkowego filmu (24 kadry na każdą sekundę filmu), a 'płynność' zapewnia odtwarzacz z programem podobnym do tych dynamicznych obrazków, które tu widzimy. W praktyce pakowanie filmu jest dużo bardziej skomplikowane, ale pojęcie odcinka pomiędzy figurami tłumaczy, że to jest możliwe.
Zamiast twierdzeń opisujących własności odcinka między figurami proponuję trzy zadania, z których najistotniejsze jest zad. 3. W nim ukryte są owe twierdzenia.
Zadania 1 i 2 pozwolą przyjrzeć się bliżej przykładom odcinków figur.
Kolejne podpunkty zadań 1 i 2 są coraz trudniejsze. Można więc opuszczać początkowe, gdy wydają Ci się za łatwe. Wystarczy poprawnie rozwiązać zadania 1n) i 2j). Gdy jednak masz z nimi kłopot, poprzednie podpunkty mogą stanowić wskazówki.
Zadanie 1. Opisz figury (1 - t) . A + t . B,
dla t = ![]() ,
dla t =
,
dla t = ![]() ,
dla t =
,
dla t = ![]() (albo ogólnie, dla dowolnego t, 0 < t < 1),
to znaczy opisz ich kształty oraz podaj obwody i pola,
(albo ogólnie, dla dowolnego t, 0 < t < 1),
to znaczy opisz ich kształty oraz podaj obwody i pola,
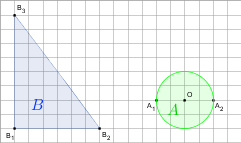
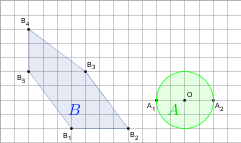
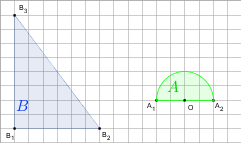
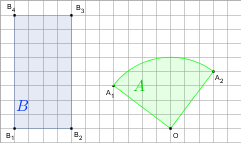
gdy A i B są takie, jak na rysunku. Przyjmij, że kratka ma wymiary 1×1.
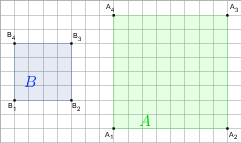 b)
b) 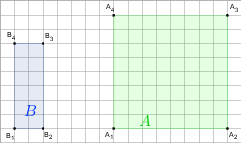
c)
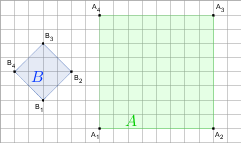 d)
d) 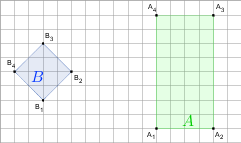
e)
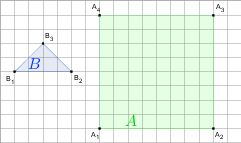 f)
f) 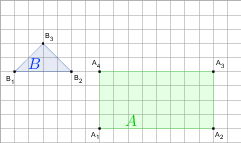
g)
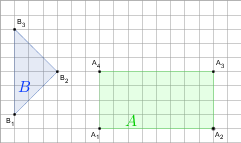 h)
h) 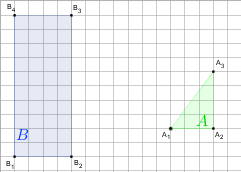
i)
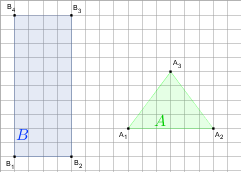 j)
j) 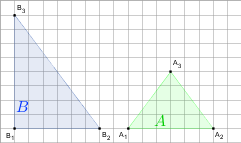
k)
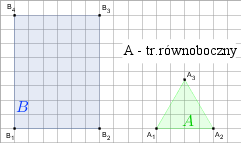 l)
l) 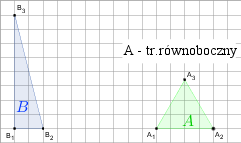
m)
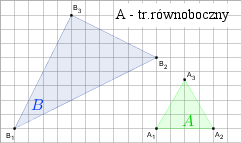 n)
n) 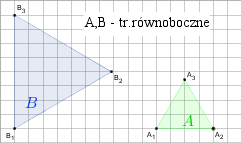
Zadanie 2. Podaj obwody i pola figur (1 - t) . A + t . B,
dla t = ![]() ,
dla t =
,
dla t = ![]() ,
dla t =
,
dla t = ![]() (albo ogólnie, dla dowolnego t, 0 < t < 1),
gdy A i B są takie, jak na rysunku. Przyjmij, że kratka ma wymiary 1×1.
(albo ogólnie, dla dowolnego t, 0 < t < 1),
gdy A i B są takie, jak na rysunku. Przyjmij, że kratka ma wymiary 1×1.
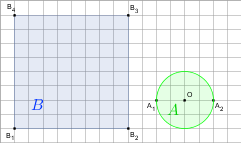 b)
b) 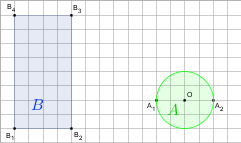
c)
 d)
d) 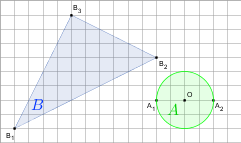
e)
 f)
f) 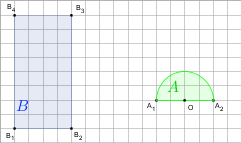
g)
 h)
h) 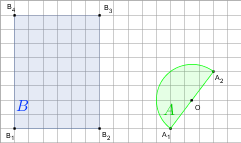
i)
 j)
j) 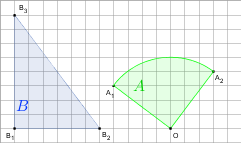
Zadanie 3. Odpowiedz na poniższe ogólne pytania. Precyzyjnie uzasadnij odpowiedź 'nie'.
a) Czy jeśli figury A i B są przystające, to każda figura odcinka AB przystaje do A?
b) Czy jeśli figury A i B są przystające, to każde dwie figury odcinka AB różne od końców A, B są przystające?
c) Czy jeśli figury A i B są podobne, to każda figura odcinka AB jest podobna do A?
d) Czy jeśli figury A i B są podobne, to każde dwie figury odcinka AB różne od końców A, B są podobne?
e) Czy jeśli figura B jest przesunięciem figury A, to każda figura odcinka AB przystaje do A?
f) Czy jeśli figury A i B są jednokładne, to każde dwie figury odcinka AB są jednokładne?
g) Czy jeśli figury A i B są wielokątami, to
h) Czy jeśli figury A i B są wielokątami wypukłymi, to
i) Czy jeśli figury A i B są wielokątami wypukłymi, to
j) Czy jeśli figury A i B są wielokątami wypukłymi, to
k) Czy jeśli A i B są odcinkami, to każda figura odcinka AB różna od końców A, B, ma dodatnie pole?
l) Czy jeśli figury A i B są wielokątami, a C jest figurą odcinka AB, to każda figura odcinka AC jest figurą odcinka AB?
m) Czy jeśli figury A i B są wielokątami wypukłymi, a C jest figurą odcinka AB, to każda figura odcinka AC jest figurą odcinka AB?
Odpowiedzi do zadania 3:
Warto przeczytać inne teksty o podobnej tematyce:
- Środki par zbiorów
- Środki zbiorów liczb
- Odcinek z funkcji
- Środki figur płaskich






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 

