Funkcja: - Dzień dobry. Nazywam się
Lekarz: - Dzień dobry.
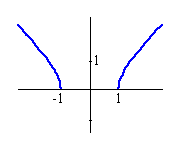 Widzę, że ma Pani kłopoty z dziedziną.
Widzę, że ma Pani kłopoty z dziedziną.
Nie trawi Pani nic z przedziału (-1, 1).
F.: - Od zawsze na to cierpiałam. Wszyscy to diagnozowali, ale dotychczas nikt nie umiał temu zaradzić.
L.: - Medycyna robi wielkie postępy. Pani dziedzina się rozszerzy, gdy będzie się Pani bezwzględnie stosować do poniższej receptury
(po 2 miesiącach)
 F.: -
Panie doktorze, czuję się jak nowonarodzona, stosując
F.: -
Panie doktorze, czuję się jak nowonarodzona, stosując
L.: -
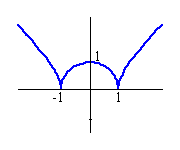
Świetnie. Właściwie jest Pani nową funkcją.
Czy teraz nie ma już żadnych dolegliwości?
F.: -
Niestety są. To zapewne skutki uboczne.
Odczuwam kłucie, o tu, w x = -1 i x = 1.
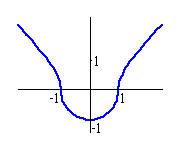 L.: -
Taaak. Widać to na wykresie.
Zatem zmienimy Pani recepturę.
L.: -
Taaak. Widać to na wykresie.
Zatem zmienimy Pani recepturę.
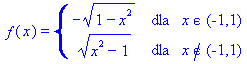 .
.(po 2 tygodniach)
F.: - Panie Doktorze, nic mnie nie kłuje. Przychodzę właściwie tylko z pytaniem. W aptece oferują mi pewien zamiennik przypisanego przez Pana specyfiku. Mianowicie
 L.: -
To jest dokładnie to samo, jeśli chodzi o działanie.
Na rynku można też znaleźć inne specyfiki.
L.: -
To jest dokładnie to samo, jeśli chodzi o działanie.
Na rynku można też znaleźć inne specyfiki.
Proszę jednak uważać i nie stosować
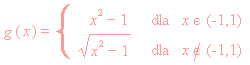 .
. Trochę inne działanie, zwłaszcza w przedziale (-5/4, 5/4), ma
Trochę inne działanie, zwłaszcza w przedziale (-5/4, 5/4), ma
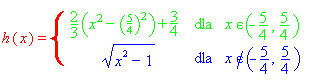 .
.





 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 

