Składanie funkcji można ćwiczyć na wzorach, algebraicznie. Jest to wówczas ćwiczenie trochę mechaniczne. Szkicowanie wykresów funkcji złożonych pozwala lepiej to pojęcie zrozumieć.
Zad. 1. Poniżej naszkicowano wykresy finkcji f1(x) oraz podano, jaką funkcją jest f2(x). Naszkicuj wykresy złożeń f2(f1(x)).
f1(x) 
f2(x) kwadrat sześcian f. wykładnicza logarytm odwrotność
f2(f1(x)) 
f1(x) 
f2(x) logarytm moduł logarytm dodanie 2 czwarta potęga
f2(f1(x)) 
Zad. 2. Który z wykresów może przedstawiać krzywą o równaniu y = sin(cos-1x)?
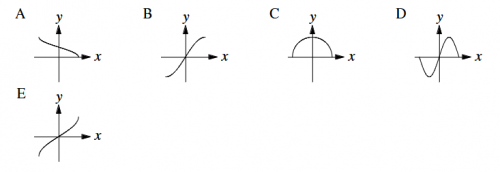
Zad. 3. Naszkicuj wykresy następujących funkcji złożonych:
a) cos(ln x) b) ln(cos x)
c) 1/sinx d)sin(1/x)
Rozwiązania
Zad. 1.
Zad. 2. Niech z=(cos-1x). Wówczas x=cos z, a y=sin z. Stąd mamy x2+y2=1. Ponadto wiemy, że z leży między 0° a 180°, x leży między -1 a 1, a y leży między 0 a 1. Szukanym wykresem jest więc górna połówka okręgu z diagramu C.
Zad. 3.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
