|
Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą. |
Każdy z poniższych wielościanów wygląda jak światowid; z każdej z 4 stron świata wygląda jednakowo. Zobacz.
Zapraszamy do zabawy, do projektowania własnych światowidów.
Na siatce 1×1 zrób swój własny projekt wielokąta P,
będącego widokiem z profilu i en face projektowanej bryły.
Automat z sześcianu 1×1×1
Pracownia projektowa ŚWIATOWIDÓW WIELOŚCIENNYCH
Uwaga. Przemieszczaj 'czarne' punkty - wierzchołki wielokąta P. Ograniczająca łamana może mieć punkty samoprzecięć pod warunkiem, że są one wyznaczone przez 'czarne' punkty.
liczba punktów: <12
Spróbujcie wyznaczyć objętości światowidów.
Wymiary projektów proszę odczytać z rysunków.
W każdym przykładzie projekt leży na kwadracie 1×1 (podzielonym kratkami na 100 części),
a światowid 'żyje' w sześcianie 1×1×1.
Zadanie 1.
Sprawdź, że poniższe światowidy mają jednakową objętość. Jaką?
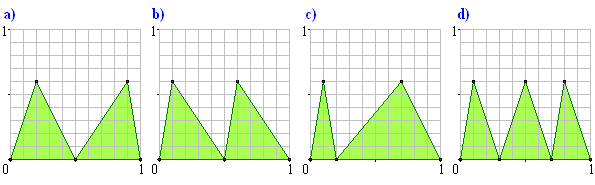
Zadanie 2.
Oblicz objętości poniższych światowidów.
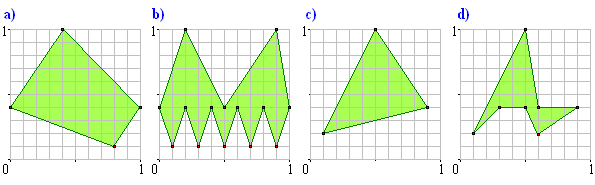
Zadanie 3.
Sprawdź, że poniższe światowidy mają jednakową objętość. Jaką?
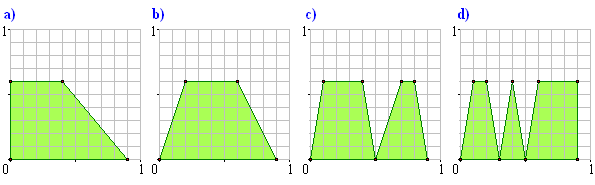
Zadanie 4.
Oblicz objętości poniższych światowidów.
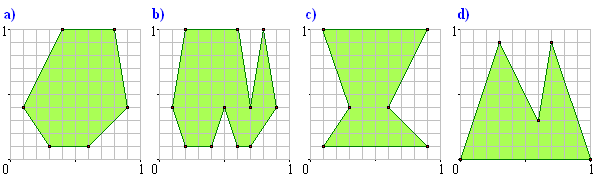
Zadanie 5*.
Oblicz objętości poniższych światowidów.
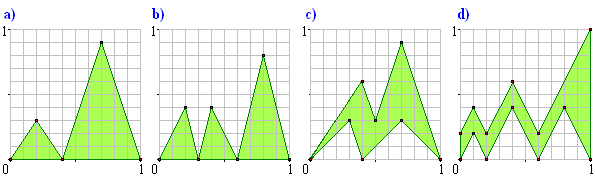
Zadanie 6*.
Wyznacz wzory na objętości poniższych światowidów.
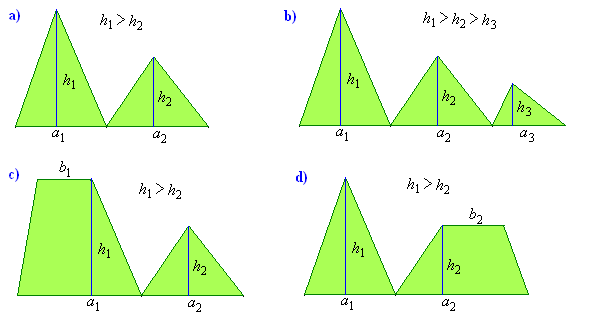
Zadanie 7**.
Znacznie trudniejsze (i bardziej żmudne) jest wyznaczanie pola powierzchni całkowitej takich brył.
Spróbujcie wyznaczyć je dla światowidów z Zadania 2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
