Rysunki utworzono za pomocą programu C.a.R. Dziękujemy Rene Grothmannowi.
Co wspólnego mają ostrosłupy i stożki?
Sporo:
- mają wyróżniony wierzchołek (W),
- mają podstawę (o polu P),
- mają wysokość (= H),
będącą odległością wierzchołka od płaszczyzny zawierającej podstawę,
- mają jednakowy wzór na objętość:
V = 1/3 P H .
Ponadto, jeśli staniemy w wierzchołku W i sfotografujemy podstawę, to zdjęcia 'zoomowane' w skalach < 1,
'wymiotą' całą bryłę.
| rys. 1.
| rys. 2.
|
Można powiedzieć (trochę bardziej skomplikowanie), że
że każdy z nich leży w płaszczyźnie odległej o H od wierzchołka W.
Bryłę spełniającą takie warunki nazwiemy stożsłupem o wierzchołku W, wysokości H i podstawie P.
Sześcian jest stożsłupem o wierzchołku w środku sześcianu i podstawie będącej całą powierzchnią sześcianu (rys. 3). Sprawdź, że wzór na objętość V = 1/3 P H jest poprawny.
Ćwiczenie 1
Jaki graniastosłup prawidłowy, sześciokątny jest stożsłupem o wierzchołku w środku graniastosłupa i podstawie będącej całą powierzchnią graniastosłupa? (patrz rys. 4)
Ćwiczenie 2
Jaki graniastosłup prawidłowy, trójkątny jest stożsłupem o wierzchołku w środku graniastosłupa i podstawie będącej całą powierzchnią graniastosłupa? (patrz rys. 4)
| rys. 3.
| rys. 4
|
Każdy wielościan opisany na kuli o środku W i promieniu r jest stożłupem o wierzchołku W i wysokości r. Podstawą takiego stożłupa jest cała powierzchnia tego wielościanu (rys. 4-5).
Ćwiczenie 3
Uzasadnij wzór na promień r kuli wpisanej w ostrosłup prawidłowy o wysokości h, o polu podstawy Ppodst. i polu powierzchni bocznej Pbocz. :
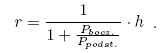
Ćwiczenie 4*
Uzasadnij wzór na promień r kuli wpisanej w ostrosłup prawidłowy o wysokości h i kącie a nachylenia ścian bocznych do podstawy:
| rys. 5.
| rys. 6.
|
Sześcian jest też stożsłupem o wierzchołku W w jednym z wierzchołków sześcianu.
Wtedy podstawa składa się z trzech ścian sześcianu, niezawierających W (rys. 7).
Sprawdź, że wzór na objętość V = 1/3 P H jest poprawny.
| rys. 7
| rys. 8.
|
Pewne graniastosłupy prawidłowe są stożsłupami o wierzchołku w środku podstawy graniastosłupa (rys. 9).
Ćwiczenie 5
Jakie wymiary ma graniastosłup prawidłowy, sześciokątny, który jest stożsłupem o wierzchołku W w środku podstawy graniastosłupa i podstawie będącej całą powierzchnią graniastosłupa z wyjątkiem ściany zawierającej W?
Ćwiczenie 6
Jakie wymiary ma graniastosłup prawidłowy, trójkątny, który jest stożsłupem o wierzchołku W w środku podstawy
graniastosłupa i podstawie będącej całą powierzchnią boczną graniastosłupa z wyjątkiem ściany zawierającej W?
| rys. 9.
| rys. 10.
|
Każdy ostrosłup prawidłowy jest stożsłupem o wierzchołku w środku podstawy ostrosłupa i podstawie będącej całą powierzchnią boczną ostrosłupa (rys. 10).
Ćwiczenie 7
Wyznacz wzór na odległość środka podstawy ostrosłupa prawidłowego od ścian bocznych tego ostrosłupa.
Ciekawie jest zobaczyć, że walec o promieniu podstawy R równym wysokości jest także stożsłupem (rys. 11).
(Kafelki, którymi wyłożona jest powierzchnia boczna walca i jedna z podstaw, leżą w płaszczyznach odległych o R od środka drugiej podstawy W walca.)
| rys. 11.
| rys. 12.
|
Zobacz, że każdy stożek prosty jest stożsłupem o wierzchołku W w środku podstawy stożka i podstawie będącej (całą) powierzchnią boczną stożka (rys. 12).
(Kafelki, którymi wyłożona jest powierzchnia boczna stożka, leżą w płaszczyznach jednakowo odległych od W .)
Kula też jest stożsłupem. O jakim wierzchołku i jakiej podstawie?
Sprawdź, że i tym razem wzór na objętość V = 1/3 P H jest poprawny.
Przykłady stożsłupów można mnożyć. Ale po co to pojęcie?
Musisz przyznać, drogi Czytelniku, że powyżej zobaczyłeś znane bryły, ale inaczej niż widziałeś je dotychczas.
Teraz widzisz więcej. To jest właśnie zasługa tego pojęcia.
Tylko tyle? To ma być cała motywacja, by wprowadzać nowe pojęcie?
Właściwie tak. Matematyka to nic innego, jak pewien sposób patrzenia. Pojęcia ułatwiają nam widzenie. Wyostrzają wzrok.
Inne przykłady stożsłupów można znaleźć w tekstach: Klina klinem, Klin ze stożka.
