Sześcian w procesie dydaktycznym

Prosta bryła, jaką jest sześcian, została tu opisana jako multiśrodek dydaktyczny rozwijający wyobraźnię i logiczne myślenie, ćwiczący biegłość rachunkową oraz pozwalający wprowadzać intuicje bardziej zaawansowanych pojęć matematycznych. Książka jest poradnikiem metodycznym, ale jej podstawową wartość stanowi bogaty zbiór problemów, ćwiczeń i gier z różnych działów matematyki szkolnej gotowych do wykorzystania w czasie lekcji na różnych etapach edukacyjnych. Jest to raczej nietypowe dla poradnika metodycznego, by niewiele miejsca poświęcał teorii nauczania, za to koncentrował się na praktyce, by był napisany prostym, zrozumiałym dla wszystkich językiem, nie popadał w przenaukowioną terminologię dydaktyczną. To właśnie dzięki tym cechom po ponad 25 latach od jego wydanie poradnik wcale się nie zestarzał i nadal powinien być wartościową i pożądaną pozycją w biblioteczce każdego nauczyciela matematyki. Mogą korzystać z niego samodzielnie także uczniowie, nawet ci
najmłodsi, traktując go jako pasjonujący zbiór zadań i łamigłowek.

Zaletami książki są też:

• różnorodność poruszanych zagadnień z zakresu szkolnej matematyki (arytmetyka, systemy liczbowe, algorytmika, logika, geometria płaska i przestrzenna, algebra, rachunek prawdodpodobieństwa czy topologia), a także tworzenie wielodyscyplinarnych powiązań między nimi (np. ćwiczenia z zakresu szkolnej arytmetyki wymagające użycia wyobraźni przestrzennej), 
• bardzo duża liczba ciekawych i urozmaiconych ćwiczeń do każdego z prezentowanych tematów,
• wysokie walory metodyczne proponowanych zadań, brak zadań schematycznych, odtwórczych i narzędziowych,
• opatrzenie wskazówkami lub przykładowymi rozwiązaniami trudniejszych zadań,
• bogactwo pomysłów na poglądowe i interaktywne wykorzystanie prostych pomocy dydaktycznych, także w formie zagadek oraz gier i zabaw dydaktycznych,
• inspiracja do tworzenia nowych ćwiczeń w podobnym duchu,
• nacisk na rozwijanie technik sprytnych rachunków,
• duża przydatność prezentowanego materiału na lecjach w szkole, zajęćiach wyrównawczych, obozach matematycznych, a także podczas ćwiczeń wykonywanych w domu,
• bogactwo kolorowych, czytelnych rysunków i materiałów typu "ready to use".

Jest to trochę już dziś zapomniana, ale z pewnością warta odkurzenia pozycja dla wszystkich nauczycieli chcących rozwijać u uczniów wyobraźnię przestrzenną, kreatywność i matematyczne myślenie, umiejętność argumetowania, uzasadniania sądów oraz wizualizowania pojęć i ich precyzyjnego definiowania. Trudno nie oprzeć się wrażeniu, że wykorzystanie różnych koncepcji sześcianu jako oprawy dydaktycznej procesu nauczania matematyki było tylko pretekstem do stworzenia niezwykle cennego zbioru zadań i pomysłów na zajęcia.

Chyba nic lepiej nie zachęci nauczycieli i rodziców do skorzystania z omawianej pozycji niż zaczerpnięte z niej ćwiczenia. Przedstawiamy dwa przykłady związane z ważnym aspektem kształcenia matematycznego obecnym na każdym etapie edukacyjnym, mianowicie z kształceniem i rozwijaniem wyobraźni przestrzennej. Czy można to zrobić lepiej? Oceńcie sami.

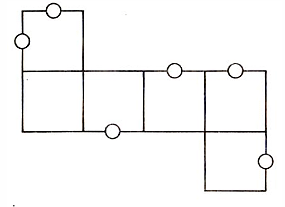
Ćwiczenie 1. Zaznacz jednakowym kolorem pary kropek, które pokryją się po złożeniu każdej z siatek w model sześcianu.

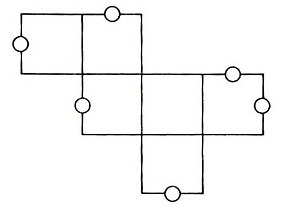
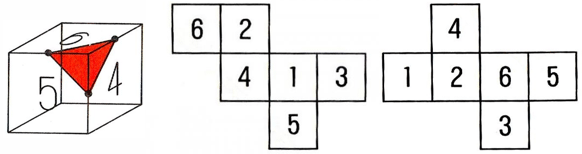
Ćwiczenie 2. Rozcięcie sześcianu płaszczyzną daje w przekroju trójkąt równoboczny (patrz rysunek poniżej). Zaznacz przebieg boków tego trójkąta na każdej z siatek sześcianu.

Jedynym mankamentem książki jest jej mało staranna redakcja językowa, skutkująca drobnymi, ale często powtarzającymi się i przez to irytującymi błędami (np. nadużywanie całkowicie zbędnego zaimka 'nasz' w określeniach: nasz sześcian, nasza kostka, nasza zabawa, nasze zadania). Mimo to jest ona bardzo przydatnym narzędziem dydaktycznym, które warto gorąco polecić. Niestety, równie ciekawa, fachowa i wartościowa pozycja od dawna nie pojawiła się na rynku wydawniczym.