Granice

...obwód największego koła, niemogącego już być większym,
jest krzywą w stopniu minimalnym,
a więc w stopniu największym jest prostą.
Mikołaj z Kuzy „O oświeconej niewiedzy”

Do końca grudnia 2015 w galerii Kino w Dolnośląskim Centrum Filmowym (budynek dawnego kina Warszawa, ul. Piłsudkiego 64a) prezentowana jest wystawa najnowszych prac multimedialnych Jakuba Jernajczyka pt. "Granice 2015". Jej wernisaż odbył się 3 XII 2015 o godz. 19:30. Wystawę można zwiedzać codziennie w godz. 10-20.

Prace w różny sposób odnoszą się do matematycznego pojęcia granicy. Można w nich odnaleźć nieustanne dążenie łuków do prostej (Granice koła), dychotomiczne podziały płaszczyzny (Zenon), nieskończone przybliżenia liczby niewymiernej (Reszta), a także dynamiczne całkowanie ciała (Ciałka oznaczone). Wystawa stanowi element realizacji interdyscyplinarnego projektu badawczego „Wizualizacja zagadnień naukowych – przykłady klasyczne w ujęciu nowych mediów cyfrowych” finansowanego przez Fundację na rzecz Nauki Polskiej.

^{Granice koła (wideoinstalacja, 2015)}

Praca odnosi się do matematyczno-filozoficznych spekulacji Mikołaja z Kuzy związanych z badaniem własności obiektów nieskończonych. W dziele "O oświeconej niewiedzy" rozważa on relacje zachodzące pomiędzy prostą a krzywą. Zauważa, że obwód największego możliwego koła (o nieskończonym promieniu) musi być tożsamy z prostą. To co Kuzańczyk mógł sobie tylko wyobrazić, dzisiaj z łatwością możemy przedstawić w postaci ruchomego obrazu. Animowana pętla ukazuje powiększające się koła, których łuki nieustannie dążą do prostej. 

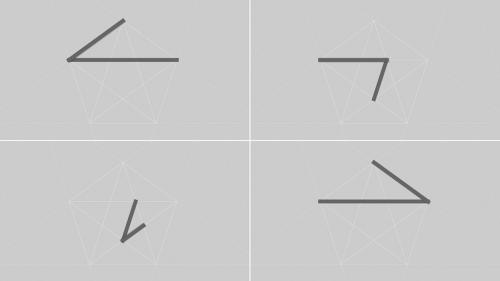
^{Reszta (instalacja multimedialna, 2014)}

Pięciokąt foremny to figura wyjątkowa. Stosunek długości jego boku do przekątnej jest równy liczbie złotej. Jest ona niewymierna, czyli nie można jej wyrazić w postaci stosunku dwóch liczb całkowitych. Algorytm Euklidesa pozwalający w przypadku liczby wymiernej w skończonej liczbie kroków znaleźć największy wspólny dzielnik licznika i mianownika można też zastosować geometrycznie do odcinków, znajdując ich proporcję. W przypadku odcinków niewspółmiernych (których stosunek długości jest liczbą niewymierną) takich jak np. bok i przekątna pięciokąta foremnego, algorytm ten nigdy się nie kończy, zawsze pozostaje niezerowa reszta.

Jakub Jernajczyk (ur. 1980 we Wrocławiu) to artysta wizualny, matematyk, popularyzator nauki. Jest adiunktem w Katedrze Sztuki Mediów wrocławskiej Akademii Sztuk Pięknych, członkiem Akademii Młodych Uczonych i Artystów. W latach 2006 i 2010 był stypendystą Ministra Kultury i Dziedzictwa Narodowego, a w 2012 roku otrzymał stypendium Ministra Nauki i Szkolnictwa Wyższego dla wybitnych młodych naukowców. Jest laureatem konkursów INTER i eNgage Fundacji na rzecz Nauki Polskiej. Uczestniczył w konferencjach naukowych i wystawach artystycznych (w m. in. w Niemczech, Rumunii, Korei Południowej, USA i Australii). W pracy twórczej skupia się na relacjach łączących sztukę z nauką, głównie z matematyką i filozofią, kładąc nacisk na poznawcze aspekty percepcji i wyobraźni wzrokowej. Jego autorska strona internetowa znajduje się pod adresem www.grapik.pl .