Tym razem zachęcamy do budowania brył, bazując nie na ich ścianach, ale na krawędziach. Moduły nie przypominają za bardzo krawędzi wielościanu, bo nie mają regularnego kształtu odcinka, dlatego z gotowego modelu czasem trudno odgadnąć, jaką bryłę przedstawia, ale tym bardziej jest on efektowny. Wykonanie pojedynczego modułu nie powinno sprawić problemów. Także łączenie elementów jest bardzo łatwe. Mając do dyspozycji odpowiednią liczbę modułów, można budować dowolnie skomplikowane bryły.
W tym artykule opiszemy dokładnie, jak zbudować z modułu krawędziowego ośmiościan foremny. A właściwie będą to aż dwa ośmiościany. Będą się różniły sposobem połączenia modułów: raz dłuższą krawędź modułu będziemy układać na zewnątrz, a raz do wewnątrz bryły. Mogłoby się wydawać, że to niewielka różnica, jednak w efekcie otrzymamy zupełnie inaczej wyglądające modele.
Legenda
Sposób wykonania pojedynczego modułu
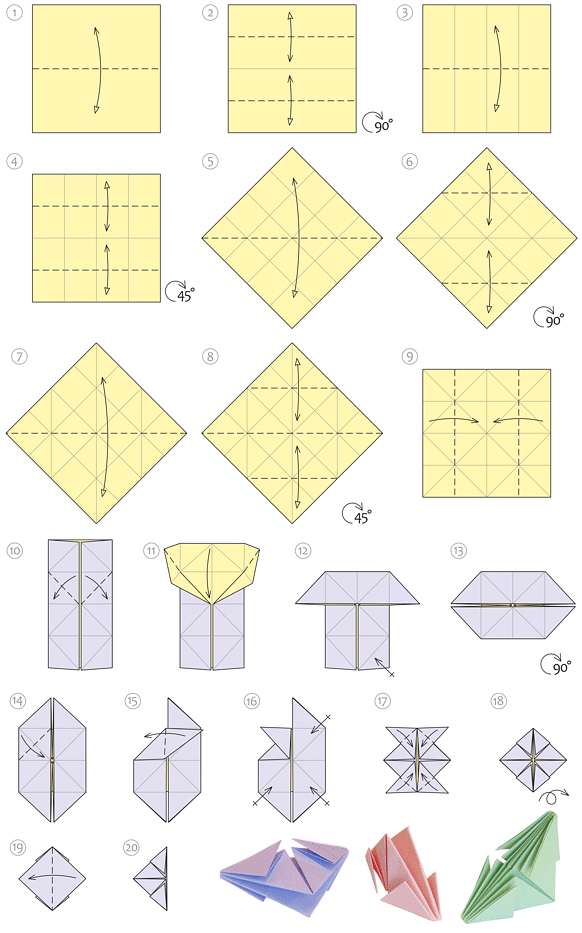
Łączenie modułów
Aby połączyć dwa moduły, trzeba rozchylić skrzydełko jednego elementu i wsunąć w nie skrzydełko drugiego. Moduły można łączyć na dwa sposoby.
I. Dłuższa krawędź do wewnątrz modelu
II. Dłuższa krawędź na zewnątrz modelu
Ośmiościan foremny
Do zbudowania ośmiościanu potrzebnych jest 12 modułów. Najlepiej wykonać je z karteczek bloczka biurowego. Zbudowana bryła będzie nieduża (ok. 6 cm wysokości), ale zgrabna.
WERSJA I
Model można dodatkowo uatrakcyjnić, zaginając fantazyjnie rogi modułów.
WERSJA II
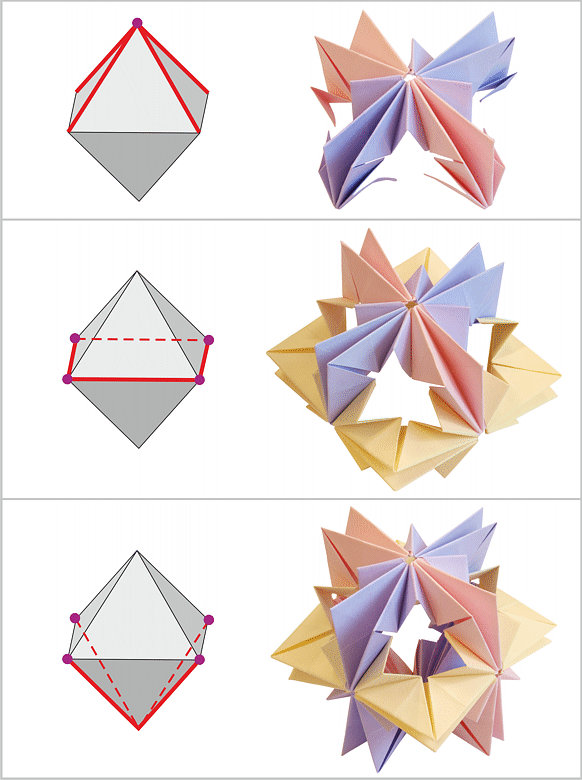
Mając gotowych kilka takich modeli, można je ze sobą łączyć. W tym celu w miejscu łączenia, zamiast normalnej krawędzi, należy użyć dwóch modułów nie zagiętych na pół (krok 18 schematu). Moduł łączący (na zdjęciu zaznaczony żółtą linią) ma 2 skrzydełka połączone z jednym modelem i 2 skrzydełka z drugim. Po drugiej stronie, analogicznie, należy wmontować drugi łącznik. Dzięki temu całość staje się bardzo solidna i stabilna.
Kilka kwadratów o różnych rozmiarach można następnie złożyć w piramidę kwadratową. Poniższa piramidka składa się z trzech luźno na siebie nałożonych warstw.
Przykłady innych brył
czworościan foremny
Prezentujemy modele otrzymane z użyciem obu sposobów łączenia modułów. Ostatni z poniższych czworościanów można zbudować, jeśli wcześniej pozagina się wierzchołki modułów.
sześcian
dwudziestościan foremny
Prace z konkursu matematycznego origami “Żuraw”
 |
 |
| Anna Kalinowska | Magdalena Karasińska |
 |
 |
| Michał Grzegorski | Michał Grzegorski |
 |
 |
| Beata Górecka-Pęder | Dorota Kęszycka |
 |
 |
| Michał Kotowski | Michał Kotowski |
Praca zbiorowa wykonana przez uczestników XXVIII Zimowej Szkoły Matematyki
Modele wykonane przez uczestników kursu wychowawców kolonijnych w IM UWr 2018
