| więcej informacji o tekście: |
Twierdzenie Ptolemeusza opisuje zależność między bokami a przekątnymi czworokąta wpisanego w okrąg. Orzeka, że iloczyn długości tych przekątnych jest równy sumie iloczynów długości przeciwległych boków tego czworokąta. Jest też prawdziwe twierdzenie odwrotne. Odkrycie tych twierdzeń i przeprowadzenie ich dowodów przypisuje się Klaudiuszowi Ptolemeuszowi (100-168) - greckiemu astronomowi, matematykowi i geografowi. Zawarł je w swoim dziele "Almagest”.
Dowód twierdzenia Ptolemeusza
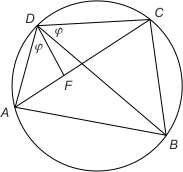
Niech F będzie takim punktem na AC, że |∡ADF| = |∡CDB|. Wówczas trójkąty ADF i DCB są podobne z cechy kkk (kąty DAC i DBC są wpisane w okrąg i oparte na tym samym łuku CD), a także trójkąty ADB i DFC są podobne (kkk). Otrzymujemy zatem równości |AD|:|AF| = |DB|:|BC| oraz |DC|:|FC| = |DB|:|AB|, a po przekształceniu |AD|·|BC| = |AF|·|DB| oraz |DC|·|AB| = |FC|·|DB|. Po dodaniu stronami ostatnich równań otrzymujemy |AD|·|BC| + |DC|·|AB| = (|AF|+|FC|)·|DB| = |AC|·|DB|, c.n.d.
Poznajmy teraz zastosowanie twierdzenia Ptolemeusza do rozwiązania szeregu ciekawych zadań z elementarnej geometrii.
Zad. 1. Niech X jest dowolnym punktem okręgu opisanego na trójkącie równobocznym ABC. Wykaż, że długość największego z odcinków XA, XB, XC jest równa sumie długości dwóch pozostałych.
Rozwiązanie. Kilkanaście dowodów tej tezy można znależć na Portalu w artykule Kopalnia metod.
Zad. 2. Okrąg przechodzący przez wierzchołek kąta odcina na jego ramionach odcinki o długościach m i n, a na dwusiecznej odcinek o długości l. Wykaż, że stosunek (m+n) : l nie zależy od położenia i promienia okręgu.

Rozwiązanie. Niech ramiona danego kąta o mierze φ przecinają okrąg w punktach B i C, a dwusieczna - w punkcie W. Zauważmy, że |CW| = |WB| = d. Z twierdzenia Ptolemeusza mamy m·d + n·d = l·|BC|, skąd (m+n):l = |BC|/d. Rozważmy trójkąt równoramienny CBW. Mamy |∡CWB| = 180°–φ oraz |∡WBC| = φ/2. Zauważmy dalej, że 1/2|BC|/d = cos(φ/2), a stąd (m+n):l = |BC|/d = 2cos(φ/2), zatem stosunek (m+n) : l zależy tylko od rozwartości danego kąta.
Zad. 3. Na przeciwprostokątnej zbudowano kwadrat na zewnątrz trójkąta. Wyznacz odległość wierzchołka kąta prostego od środka tego kwadratu, wiedząc że suma długości przyprostokątnych wynosi m.
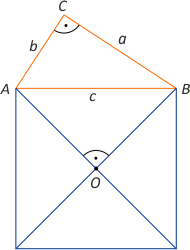
Rozwiązanie. Niech w trójkącie ABC (o bokach długości a, b, c) kąt C jest prosty. Środek kwadratu O jest punktem przecięcia jego przekątnych, a te są prostopadłe. Oznacza to, że na czworokącie CAOB można opisać okrąg i z twierdzenia Ptolemeusza otrzymujemy c·|CO| = 1/2·a·c√2+ 1/2·b·c√2, skąd mamy |CO| = 1/2·(a+b)√2 i ostatecznie wobec założenia |CO| = 1/2·m·√2.
Zad. 4. Trójkąt ABC wpisano w okrąg. Oznaczmy przez m, n, k odległości pewnego punktu X
leżącego na okręgu od prostych zawierających odpowiednio boki BC, AC, AB. Wykaż, że a/m = b/n + c/k , gdzie a, b, c to odpowiednio długości boków BC, AC, AB.
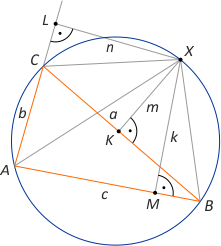
Rozwiązanie. Rozważmy czworokąt ABXC. Z twierdzenia Ptolomeusza mamy (*) a·|AX| = b·|XB| + c·|XC|. Niech M, K i L będą rzutami punktu X odpowiednio na boki AB, BC i AC. Zauważmy, że kąty CAX i CBX są przystające, bo są oparte na tym samym łuku CX. Stąd trójkąty prostokątne XLA i XKB są podobne. Równe miary mają też kąty wpisane XCB i XAB, skąd wynika, że podobne są trójkąty prostokątne CKX oraz AMX. Otrzymujemy zatem proporcje |XB|:m = |AX|:n oraz |XC|:m = |XA|:k, skąd |XB| = m|AX|/n oraz |XC| = m|AX|/k. Po podstawieniu do (*) mamy a·|AX| = b·(m|AX|/n) + c·(m|AX|/k). Dzieląc obie strony tej równości przez m|AX|, otrzymujemy a/m = b/n + c/k.
Zad. 5. Niech ABCDEFG będzie siedmiokątem foremnym. Wykaż, że 1/|AC| + 1/|AD| = 1/|AB|.
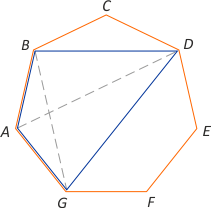
Rozwiązanie. Siedmiokąt foremny można wpisac w okrąg, a zatem także każdy czworokąt wybrany spośród jego 7 wierzchołków. Wystarczy teraz zastosować twierdzenie Ptolomeusza np. do czworokąta ABDG. Zauważmy, że |AB|=|AG|=a, |BG|=|BD|= b i |AD|=|GD|=c. Mamy c·b = a·b + a·c. Dzieląc obie strony tej równości przez a·b·c, otrzymujemy 1/a = 1/b + 1/c, a to jest właśnie teza zadania.
Zad. 6. Długości boków trójkąta ABC tworzą ciąg arytmetyczny (b>a>c). Pokaż, że jeśli na trójkącie opiszemy okrąg i przedłużymy dwusieczną AI do przecięcia z okręgiem w punkcie W1, to |AI| = |IW1|, gdzie I to środek okręgu wpisanego w trójkąt (tzw. incentrum trójkąta).

Rozwiązanie. Odcinki W1B i W1C są przystające, jako cięciwy, na których są oparte przystające kąty wpisane w okrąg. Stosując twierddzenie Ptolomeusza do czworokąta ABW1C, mamy a·|AW1| = b·|W1B| + c·|W1C| = (b+c)|W1B|. Korzystając z tzw. własności trójliścia, zgodnie z którą |BW1|=|IW1| - dowód w zad. 8 w artykule Z okręgiem Eulera w tle, otrzymujemy a·|AW1| = (b+c)·|IW1|. Z załozenia b+c = 2a, zatem |AW1| = 2|IW1|. Stąd I jest środkiem odcinka AW1, co kończy dowód.
Zad. 7. Wykaż, że w trójkącie ostrokątnym suma odległości środka okręgu opisanego na trójkącie od boków tego trójkąta jest równa sumie długości promieni okręgów opisanego na trójkącie i wpisanego w trójkąt.

Rozwiązanie. Rozważmy czworokąt AM3OM2. Można na nim opisać okrąg, bo suma miar kątów AM3O i AM2O wynosi 180°. Stosując twierdzenie Ptolomeusza, otrzymujemy |AO|·|M2M3| = |AM2|·|OM3| + |AM3|·|OM2| lub inaczej, korzystając z własności linii środkowej trójkąta (odcinek łączący środki dwóch boków jest dwa razy krótszy od trzeciego), mamy R·a/2 = b/2·|OM3| + c/2·|OM2|. Analogicznie mamy R·b/2 = a/2·|OM3| + c/2·|OM1| oraz R·c/2 = b/2·|OM1| + a/2·|OM2|. Dodając stronami te równości, otrzymujemy R/2·(a+b+c) = 1/2·(a+b)·|OM3| + 1/2·(a+c)·|OM2| + 1/2·(b+c)·|OM1|. Dodając teraz do każdej ze stron pole trójkąta ABC wyrażone innym wzorem, otrzymujemy R/2·(a+b+c) + r/2·(a+b+c) = 1/2·(a+b)·|OM3| + 1/2·(a+c)·|OM2| + 1/2·(b+c)·|OM1| + c/2·|OM3| + a/2·|OM1| + b/2·|OM2|. Po drobnych przekształceniach ostatecznie otrzymujemy 1/2·(a+b+c)·(R+r) = 1/2·(a+b+c)·(|OM1|+|OM2|+|OM3|), skąd wynika teza.
Zad. 8. W trójkąt ABC wpisano półkole tak, że średnica półkola zawiera się w boku BC, a F1 i F2 to punkty styczności półkola z bokami AB i AC. Dwusieczna kąta BAC przecina okrąg opisany na trójkącie w punkcie W1. Wykaż, że pole trójkąta ABC wynosi 1/2|F1F2|·|AW1|.
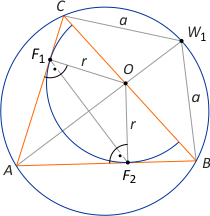
Rozwiązanie. Oznaczmy |WC|=|WB|=a i |OF1|=|OF2|= r. Zauważmy, że kąty F1OF2 i BW1C są przystające, bo ich miary uzupełniają miarę kąta BAC do 180° (w czworokątach AF1OF2 i ABW1C). Stąd trójkaty równoramienne F1OF2 i BW1C są podobne w skali k = r/a = |F1F2|/|BC|. Stąd mamy r = a·|F1F2|/|BC|. Zauważmy dalej, że PABC = PABO + PAOC = r/2·(|AB|+|AC|) = 1/2·(a·|F1F2|/|BC|)·(|AB|+|AC|). Stosując twierdzenie Ptolomeusza do czworokąta ABW1C, mamy a·(|AB|+|AC|) = |BC|·|AW1| i po podstawieniu do poprzedniej równości otrzymujemy PABC = 1/2|F1F2|·|AW1|.
Zad. 9. W trójkącie ABC (o bokach długości a, b i c) punkty A, M2, M3 i L1 leżą na jednym okręgu (punkty M2 i M3 to odpowiednio środki boków AC i AB, a L1 to punkt przecięcia dwusiecznej kąta BAC z BC). Wykaż, że a√2 = b + c.
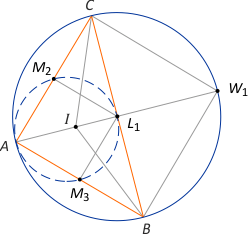
Rozwiązanie. Łatwo zauważyć, że okręgi AM3L1M2 i ABW1C są jednokładne w skali 1/2 względem wierzchołka A. Stosując twierdzenie Ptolomeusza do czworokąta ABW1C, mamy a·|AW1| = b·|W1B| + c·|W1C|. Korzystając (jak w zad. 6 powyżej) z własności trójliścia, otrzymujemy a·|AW1| = (b+c)·|IW1|, skąd |IW1|:|AW1| = a:(b+c). Dalej |AL1|:|AW1| = 1/2 = (|AI|+|IL1|):|AW1| = (|AW1|–|IW1|+|IL1|):|AW1| = 1–a/(b+c)+|IL1|:|AW1|. Z twierdzenia o dwusiecznej kąta dla trójkątów ABL1 i ACL1 mamy |AI|:|IL1| = c:|BL1| = b:|CL1|, a z proporcji mamy |AI|:|IL1| = (c+b):(|BL1|+|CL1|) = (b+c):a. Stąd |IL1| = a·|AI|/(b+c) i dalej |IL1|:|AW1| = (a/(b+c))·(|AI|/|AW1|) = (a/(b+c))·(|AW1|–|IW1|)/|AW1| = (a/(b+c))·(1– a/(b+c)). Ostatecznie otrzymujemy 1/2 = 1–a/(b+c)+(a/(b+c))·(1–a/(b+c)), czyli 1/2 = ((b+c)2–a2)/(b+c)2, skąd po przekształceniach mamy tezę.
Zad. 10. Proste wyznaczone przez dwusieczne kątów A, B i C trójkąta ABC przecinają okrąg opisany na tym trójkącie odpowiednio w punktach W1, W2 i W3. Udowodnij, że |AW1|+|BW2|+|CW3| > |AB|+|BC|+|AC|.
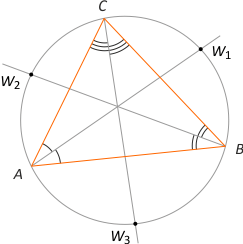
Rozwiązanie. Oznaczmy |W1C|=|W1B|=d. Z twierdzenia Ptolemeusza w czworokącie ABW1C mamy a·|AW1| = d(b+c). Z nierówności trójkąta mamy 2d>a, skąd d/a > 1/2. Otrzymujemy zatem |AW1| > 1/2(b+c) oraz analogicznie |BW2| > 1/2(a+c) i |CW3| > 1/2(a+b). Po dodaniu tych nierówności stronami otrzymujemy tezę.







