KONKURSY › Interdyscyplinarne

Międzygimnazjalny Interdyscyplinarny Konkurs o Laur Hugona (VI)

Data ostatniej modyfikacji:
2012-05-16
Autor: 
Joanna Polechońska
nauczycielka w Gimnazjum nr 1 we Wrocławiu
Organizator: 

Gimnazjum nr 1
im. Hugona Dionizego Steinhausa
ul. Jelenia 7, 54-242 Wrocław
www.gimn1.wroclaw.pl

 

Terminy: 

zgłoszenia szkół: do 16 III 2012
eliminacje szkolne: 27 III 2012
finał w Gimnazjum nr 1 - 14 V 2012

strona domowa Konkursu

 

 

Konkurs jest bardzo ciekawy ze względu na nietypową formułę finału, w którym rozwiązywane są praktyczne interdyscyplinarne problemy. Ich geneza ściśle wiąże się z osobą bohatera konkursu. Konkurs rozwija twórcze myślenie, łączy wiedzę z zakresu różnych przedmiotów szkolnych, integruje uczniów i przybliża sylwetkę i osiągnięcia Hugona Steinhausa.

 

Historia: 

Konkurs organizowany jest od 2007 roku. Oto zwycięzcy kolejnych edycji:

  • I - 2007 - GIM ATUT Wrocław
    Oliwer Czyż, Emilia Kopeć, Paweł Stopa
  • II - 2008 - GIM ATUT Wrocław
    Michał Balicki, Katarzyna Beker, Oliwer Czyż, Dorian Turkiewicz
  • III - 2009 - GIM ATUT Wrocław
    Michał Balicki, Marek Granowicz, Hubert Jarosz, Nel Krzywda-Pogorzelska
  • IV - 2010 - GIM 2 Wołów
    Kacper Grobelny, Alex Piętoń, Marcin Muszyński, Monika Toczek
  • V - 2011 - GIM 48 Wrocław
    Michał Bogacz, Michał Kotleszka, Kamil Kundera, Kacper Kuszczyński
  • VI - 2012 - Niepubliczne GIM Wołów
    Natalia Gmur, Olga Gumienna, Noemi Nejman, Maria Stodolna

Po zawodach odbyły się odczyty:

  • 2007 - Małgorzata Mikołajczyk IM UWr Wielokąty gwiaździste,
  • 2008 - Małgorzata Mikołajczyk IM UWr Ćwiczenia ze wstążką,
  • 2009 - Małgorzata Mikołajczyk IM UWr, Skąd się biorą duże liczby?
  • 2010 - Małgorzata Mikołajczyk, IM UWr, O sprawiedliwym podziale
  • 2011 - Adam Morawiec, IM UWr, Ten zegar stary...
  • 2012 - Adam Morawiec, IM UWr, Hugo Steinhaus i jego wynalazki

Uroczyste zakończenie konkursu uświetniają występy szkolnego chóru kameralnego i zespołu tańca nowoczesnego - oba pod kierunkiem p. Piotra Jarońskiego.   




Zamieszczone zdjęcia pochodzą z rozgrywek w 2008 roku.

 

Skrót regulaminu: 
  • Gimnazja wrocławskie otrzymają zawiadomienia i kartę zgłoszenia, którą należy odesłać faksem, elektronicznie lub pocztą.
  • W eliminacjach uczniowie rozwiązują indywidualnie w swoich szkołach w czasie 45 minut test międzyprzedmiotowy, sprawdzający wiedzę z przedmiotów matematyczno-przyrodniczych i humanistycznych, umiejętność szyfrowania i twórcze myślenie. Karty odpowiedzi wysyła się organizatorowi najpóźniej następnego dnia po konkursie.
  • Do finału wchodzi z każdej szkoły czteroosobowa drużyna.
  • W finale drużyny rozwiązują zadania praktyczne z zakresu przedmiotów matematyczno-przyrodniczych i humanistycznych, sprawdzana jest też umiejętność szyfrowania oraz znajomość życia i twórczości Hugona Dionizego Steinhausa.
  • Po części konkursowej zawodnicy i ich opiekunowie uczestniczą w wykładzie popularnonaukowym, po którym ogłaszane są wyniki.
  • Zwycięzca otrzymuje główną nagrodę - statuetkę Hugona.

 

Przykładowe zadania: 

ELIMINACJE

1. Rysunek przedstawia różne ułożenia dwóch metalowych klocków na poziomej, metalowej płycie. Siła potrzebna do wprawienia ich w ruch będzie: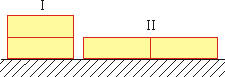
A) mniejsza w I przypadku
B) mniejsza w II przypadku
C) jednakowa w obu przypadkach
D) odpowiedź zależy od rodzaju metalu, z jakich wykonane są klocki
E) inna odpowiedź

2. Uczeń rozwiązując zadanie napisał: $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ .
Jakie warunki spełniały liczby a i b, jeżeli wynik był prawidłowy?
A) a = -b
B) a = b
C) a·b = 0
D) a i b są kwadratami liczb naturalnych
E) inna odpowiedź

3. W ośmiokącie foremnym poprowadzono dwie równoległe najdłuższe przekątne. Jaką częścią pola ośmiokąta jest pole figury jaką wycięły one z tego ośmiokąta?

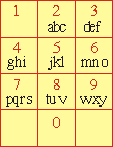
4. Cyfrom przyporządkowane są kolejne litery tak jak na klawiaturze telefonu. Co to za wyraz: 526487?

FINAŁ

1. Hugonotki. Z poniższej rozsypanki wyrazowej ułóż 8 hugonotek, z których słynął Steinhaus.

2. Hugonotki mix. Pięć aforyzmów Hugona Steinhausa zostało pomieszanych, tak że powstało pięć nowych myśli. Przywróć właściwe brzmienie aforyzmom Steinhausa.

  • Człowiek selekcjonuje automatycznie i bezbłednie adresatów.
  • Dowcip jest szyfrem, aby uczyć matematyki innych.
  • Dlaczego ludzie uczą się matematyki? Dzięki rozpowszechnieniu oświaty.
  • Jedną z cech głupstwa jest, (że) można dziś czytać, pisać i publikować, nie przestajac być analfabetą.
  • Logika jest dowodem boskości zwierzęcia.    

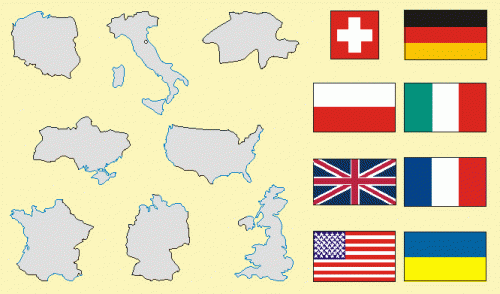
3. Państwa. Steinhaus wiele podróżował. W młodości zdobywał wykształcenie na uczelniach polskich i zagranicznych, a będąc znanym matematykiem był często zapraszany na konferencje i wykłady. Dopasuj kontury, flagi i nazwy państw, które odwiedzał Steinhaus.

4. Atbasz. To jeden z najstarszych szyfrów wymyślony przez Hebrajczyków 500 lat p.n.e. Wykorzystywał on 22 litery alfabetu hebrajskiego i był przykładem tzw. szyfru rotacyjnego, w którym pierwszą literę zastępowano ostatnią, drugą przedostatnią itd. Stosując tę zasadę przetłumacz i wykonaj zakodowane polecenie.
ŻEŹŃJGJĆBYTÓĆŻEFUJHJJRTMCPYJHŻHDMFJGEFJNTUJŁHTNDCL
ÓNTEFŻNHOTĆJGJNJŃYŹOŻĆCAD

5. Chiński tangram. Ze wszystkich klocków tangramu ułóż figurę osiowosymetryczną (różną od kwadratu).

6. Sprawiedliwy podział. Kielich w kształcie stożka jest wypełniony po brzegi winem. Piotr i Jan chcą się podzielić napojem sprawiedliwie. Piotr zaproponował, aby Jan podzielił sok, a on wybierze swoją porcję. Jan przelał do drugiego naczynia tyle wina, że część pozostała w kielichu sięgała 3/4 wysokości. Piotr wybrał to, co pozostało w kielichu. Czy dobrze zrobił? Uzasadnij odpowiedź.  

 

Powrót na górę strony