Łowcy Talentów JERSZ
ul. Dębowa 2, Wilczyn, 55-120 Oborniki Śląskie
tel./faks 71 310 48 17, tel. kom. 501 101 866, 505 138 588
e-mail: biuro@jersz.pl
zgłoszenia: 8 III 2023
konkurs: 22 III 2023
Konkurs Mat został zawieszony w 2021 roku po 22 edycjach. W jego miejsce powołano w 2022 roku konkurs MATEMATIX, skierowany do uczniów szkół podstawowych i średnich. Ma formę testu wielokrotnego wyboru. Uczniowie oceniają go jako dość trudny (np. w porównaniu z Kangurem), ale ciekawy. 
Cieszy się on dużą popularnością. Zadania są zróżnicowane pod względem tematyki i trudności, często zaskakują swoją nietypowością.
W latach 1999-2020 co rok na wiosnę organizowany był konkurs MAT. W 2021 roku jego 23 edycja została odwołana i od tej pory konkurs jest zawieszony. Od 2022 roku w jego miejsce odbywa się konkurs MATEMATIX.
- Warunkiem przystąpienia szkoły do konkursu jest udział minimum 11 uczniów oraz wysłanie zgłoszenia do organizatora konkursu na trzy tygodnie przed konkursem (pocztą, faksem lub e-mailem) na karcie dostępnej na stronie organizatora. W przypadku mniejszej liczby uczestników szkoły mogą zgłaszać się wspólnie.
- Konkurs odbywa się we wszystkich szkołach w tym samym czasie. Wszystkie odstępstwa od tej reguły muszą być wcześniej zatwierdzone przez organizatora.
- Test trwa 90 minut, jest wielokrotnego wyboru i zawiera (w zależności od poziomu) 20-26 pytań z odpowiedziami A, B, C, D.
- Na starcie każdy uczestnik dostaje tyle punktów, ile ma decyzji do podjęcia (np. z kl. III SP 20 ? 4 = 80 pkt). Za każdą poprawną odpowiedź otrzymuje dodatkowo 1 pkt, za brak odpowiedzi 0 pkt, a za błędną odpowiedź (-1) pkt.
- Odpowiedzi zakreślane są na specjalnych kartach, które po zawodach przesyła się organizatorowi do sprawdzenia.
- Opłatę wnosi się na konto organizatora tuż po konkursie. Wynosi ona:
9,50 zł, gdy uczestników jest od 11 do 30,
9,25 zł, gdy uczestników jest od 31 do 60,
9,00 zł, gdy uczestników jest więcej niż 60,
10,00 zł, gdy zgłoszenia dokonano po terminie lub gdy liczba startujących zmniejszy o 10% w stosunku do podanej w zgłoszeniu.
Zwyczajowo szkoły zbierają po 7 zł i w zależności od liczby uczestników zostają im pieniądze, którą przeznaczają na koszty organizacyjne i szkolne nagrody. - Organizator na nagrody przeznacza 55% zebranych pieniędzy, a reszta pokrywa koszty organizacyjne konkursu.
- Zwycięzcy otrzymują nagrody rzeczowe oraz możliwość udziału w wycieczkach, obozach wypoczynkowo-naukowych w czasie wakacji.
SZKOŁA PODSTAWOWA
klasa 3
1. Uczniów pewnej klasy można podzielić na 3-osobowe grupy i nikt nie zostanie bez przydziału. Gdybyśmy chcieli podzielić uczniów tej klasy na 2-osobowe grupy, to jedna osoba zostanie bez pary. Ilu uczniów może liczyć ta klasa?
A) 21, B) 24, C) 27, D) 29.
2. Kilku kupców podzieliło między siebie kwadratową łąkę w taki sposób, że każdy z nich otrzymał kwadratową działkę tej samej wielkości. Ilu kupców mogło nabyć tę łąkę?
A) 4, B) 9, C) 16, D) 36.
3. Jaki wynik możemy otrzymać z dodawania jednej liczby trzycyfrowej i trzech liczb dwucyfrowych?
A) 123, B) 154, C) 201, D) 111.
klasa 4
1. Nastoletni brat Grzegorza jest od niego o 5 lat młodszy. Ile lat może mieć Grzegorz?
A) 18, B) 23, C) 30, D) 27.
2. Kasia ma w portmonetce pięć monet. Ile może mieć pieniędzy?
A) 2 zł, B) 3 zł, C) 4 zł, D) 5 zł.
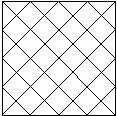3. Jeśli kwadrat z rysunku rozetniemy wzdłuż zaznaczonych linii, to:
A) wśród otrzymanych części będą 24 kwadraty,
B) wśród otrzymanych części będzie 20 trójkątów,
C) z uzyskanych części będzie można ułożyć 32 jednakowe kwadraty,
D) z uzyskanych części będzie można ułożyć (wykorzystując wszystkie części) 2 jednakowe kwadraty.
4. Suma dziewięciu różnych parzystych liczb dodatnich może być równa:
A) 86, B) 92, C) 98, D) 102.
klasa 5
1. Dziesięciozłotowy banknot rozmieniono na 5 monet. Jaka moneta na pewno wystąpiła wśród tych pięciu?
A) 50-groszowa, B) 1-złotowa, C) 2-złotowa, D) 5-złotowa.
2. Mamy do dyspozycji 5 zielonych półkul, 4 czerwone, 6 niebieskich i 3 żółte. Z każdej pary półkul można zmontować całą kulę. Czy możemy zmontować z tych połówek kule (wykorzystując wszystkie połówki) w taki sposób, by:
A) żadna kula nie składała się z dwóch połówek tego samego koloru,
B) każda kula składała się z dwóch połówek tego samego koloru,
C) było więcej kul z czerwoną połówką, niż kul z zieloną połówką,
D) każda kula zawierała albo połówkę żółtą albo połówkę niebieską.
3. Państwo Kowalscy mają czwórkę dzieci: ich dwie córki mają razem 12 lat, zaś dwaj synowie mają łącznie 26 lat. Wiemy też, że spośród ich dzieci najstarsze są bliźniaki. Jaka może być płeć tych bliźniaków?
A) 2 chłopcy, B) 2 dziewczynki, C) chłopiec i dziewczynka, D) dane są sprzeczne.
klasa 6
1. W pudełku są klocki czerwone, zielone i niebieskie. Połowa spośród tych klocków, które nie są niebieskie ? jest czerwona. Połowa spośród klocków, które nie są czerwone ? jest zielona. W takim razie:
A) w każdym z tych trzech kolorów może być inna liczba klocków,
B) w każdym z tych trzech kolorów musi być ta sama liczba klocków,
C) klocków niebieskich może być dwa razy więcej niż czerwonych,
D) klocków czerwonych może być mniej niż zielonych.
2. Chcemy rozciąć kwadrat na mniejsze kwadraty, ale w taki sposób, by wśród otrzymanych kawałków były kwadraty najwyżej dwóch różnych rozmiarów. Ile części można otrzymać z takiego rozcięcia?
A) 4, B) 6, C) 15, D) 20.
3. Jacek pomyślał pewną liczbę naturalną, podniósł ją do kwadratu, a następnie otrzymany wynik podzielił przez połowę pomyślanej liczby. Jaki wynik dzielenia mógł otrzymać?
A) 12, B) 8, C) 16, D) 5.
GIMNAZJUM
klasa 1
1. Z 2006 jednostkowych sześcianików można skleić większy sześcian (nie trzeba wykorzystywać wszystkich sześcianików), którego objętość będzie się mieściła w przedziale:
A) [1001, 1300], B) [1301, 1600], C) [1601, 1900], D) [1901 do 2006].
2. Które z poniższych zdań są prawdziwe?
A) o godzinie 15:00 wskazówki zegara są prostopadłe,
B) o godzinie 16:00 kąt między wskazówkami zegara ma miarę 120?,
C) o godzinie 18:00 kąt między wskazówkami zegara jest półpełny,
D) o godzinie 21:00 kąt między wskazówkami zegara ma miarę 120?.
3. Który z prostokątów o podanych wymiarach można rozciąć na trzy kwadraty?
A) 3 cm × 9 cm, B) 2 cm × 3 cm, C) 3 cm × 4 cm, D) kwadrat o boku 3 cm.
klasa 2
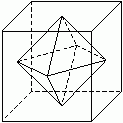1. W sześcianie pokazanym na rysunku poniżej połączono środki ścian otrzymując pewien wielościan wypukły. Wielościan ten ma:
A) dokładnie 6 ścian trójkątnych,
B) jedną ścianę czworokątną,
C) 18 krawędzi,
D) objętość 6 razy mniejszą od objętości owego sześcianu.
2. W który z wymienionych czworokątów zawsze można wpisać okrąg?
A) trapez, B) równoległobok, C) romb, D) prostokąt.
3. Istnieje para liczb całkowitych dodatnich, których iloczyn jest 2 razy większy od ich ilorazu taka, że:
A) obie liczby są nieparzyste,
B) obie liczby są tej samej parzystości,
C) jedna z tych liczb jest niewymierna,
D) dokładnie jedna z tych liczb jest parzysta.
klasa 3
1. Jaki może być obwód prostokąta o tej własności, że zarówno długości boków, jak i długość przekątnej są liczbami naturalnymi?
A) 14, B) 17, C) 24, D) 34.
2. Jacek, Staszek i Wojtek sklejają modele samolotów. Najwięcej samolotów ma Jacek i ma on tyle razy więcej modeli od Staszka, ile razy więcej modeli ma Staszek od Wojtka. Ile modeli samolotów mogą mieć łącznie trzej chłopcy, jeśli Wojtek ma cztery modele?
A) 28, B) 52, C) 8, D) 19.
3. Piotrek pomyślał pewną liczbę, podniósł ją do kwadratu, a następnie wyciągnął pierwiastek kwadratowy z wyniku. Okazało się, że otrzymał liczbę, o której wcześniej pomyślał. O jakiej liczbie pomyślał Piotrek?
A) mogła to być dowolna liczba rzeczywista,
B) musiała to być liczba dodatnia,
C) musiała to być liczba ujemna,
D) mogła to być liczba niedodatnia.
LICEUM
klasa 1
1. Którą z poniższych liczb można przedstawić w postaci sumy kwadratów czterech (niekoniecznie różnych) liczb całkowitych?
A) 96, B) 97, C) 98, D) 99.
2. W urnie są 3 białe kulki i 4 kulki czerwone. W każdym momencie możemy zamienić 3 kulki białe na 4 czerwone lub 3 kulki czerwone na 4 białe. Po pewnej liczbie takich zamian w urnie mogą się znaleźć:
A) same białe kulki,
B) same czerwone kulki,
C) dokładnie tuzin kulek,
D) 6 kulek czerwonych.
3. Wszystkie ściany pewnego wielościanu są przystającymi wielokątami foremnymi. Wiemy też, że w każdym wierzchołku schodzą się dokładnie trzy ściany. Ściany tego wielościanu mogą być:
A) trójkątami równobocznymi,
B) kwadratami,
C) pięciokątami foremnymi,
D) sześciokątami foremnymi.
klasa 2 i 3
1. W ostrokątnym trójkącie ABC, który nie jest równoramienny, wybrano punkt D, tak że trójkąty ABD, BCD, CAD są równoramienne rozwartokątne. Punkt D może być:
A) punktem przecięcia środkowych trójkąta ABC,
B) punktem przecięcia dwusiecznych kątów trójkąta ABC,
C) puntem przecięcia symetralnych boków trójkąta ABC,
D) punktem przecięcia wysokości trójkąta ABC.
2. Jaką cyfrę jedności może mieć iloczyn dwóch dwucyfrowych liczb pierwszych?
A) 2, B) 3, C) 5, D) 7.
3. Jacek pomnożył pewną liczbę naturalną przez sumę jej cyfr (w zapisie dziesiętnym). Jaką resztę z dzielenia przez 9 mogła dawać otrzymana przez niego liczba?
A) 4, B) 5, C) 6, D) 7.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
