ROZMAITOŚCI › Leksykon matematyczny

Funkcja

Data ostatniej modyfikacji:
2018-09-27
Autor: 
Sebastian Guz
student matematyki na UWr
Dział matematyki: 
funkcje

Definicja:
Przyporządkowanie elementom jednego zbioru X elementów drugiego zbioru Y w taki sposób, że każdemu elementowi x$\in$X odpowiada dokładnie jeden element y$\in$Y.

 

Definicja alternatywna:
Każdy zbiór f par uporządkowanych (x, y) takich, że  x$\in$X i y$\in$Y o tej własności, że dla każdego elementu x istnieje dokładnie jeden element y taki, że (x, y)$\in$f. Zatem jeżeli  (x, y)$\in$f oraz (x, z)$\in$f, to y = z.

 

Pojęcia równoznaczne:
odwzorowanie, operacja, przekształcenie

 

Oznaczenia:
Funkcje zwyczajowo oznacza się małymi lub dużymi literami alfabetu łacińskiego, najczęściej f, g, h, F, G, H, czasem także literami alfabetu greckiego Γ, φ, ζ.

f : X $\rightarrow$ Y - funkcja f ze zbioru X w zbiór Y

X$\ni$x$\rightarrow$f(x)$\in$Y - f przeształca X w Y

 

Elementy składowe funkcji:

Zbiór X nazywamy dziedziną (zbiorem argumentów) funkcji f i oznaczamy $D_f$ albo $dom(f)$, każdy jego element x nazwiemy argumentem. Zbiór Y to przeciwdziedzina. Fakt, że $(x,y)\in f$ zapisuje się jako $f(x)=y$ i odczytuje: "wartością funkcji f dla argumentu x jest y". Zbiór wszystkich wartości funkcji oznacza się czasami jako $rng(f)$.

Obrazy i przeciwobrazy zbiorów:

Jeżeli $A\subset X$, to obrazem f[A] zbioru A przez funkcję f:X$\rightarrow$Y nazywamy zbiór wartości funkcji , gdy argumenty przebiegają zbiór A. Wobec czego: $f[A]= \{ f ( x ) : \; x \in A \}.$
Dowodzi się, że obraz sumy zbiorów jest sumą ich obrazów, a gdy f jest różnowartościowa, analogiczne twierdzenie zachodzi dla części wspólnej zbiorów.

Jeżeli $B\subset Y$, to przeciwobrazem f-1[B] zbioru B przez funkcję f:X$\rightarrow$Y nazywamy zbiór tych argumentów funkcji f, których wartości należą do zbioru B. Wobec czego: $f^{-1} [B] = \{x \in X: \; f(x) \in B \} .$
Dowodzi się, że przeciwobraz sumy (części wspólnej) zbioró .w jest sumą (częścią wspólną) ich przeciwobrazów.

 

Sposoby opisu funkcji:

Graficznie funkcję $f$ o zbiorze wartości $D_f$ można przedstawić jak niżej:

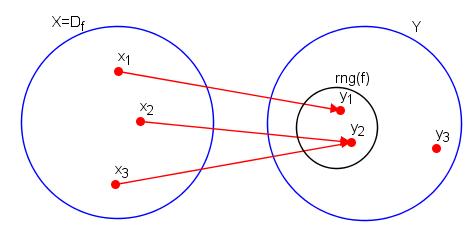
Jak  widać przeciwdziedzina i zbiór wartości funkcji nie muszą być równe.


  • słownie, np.: "dziedziną X niech będzie zbiór klientów pewnego banku posiadających rachunki oszczędnościowo-rozliczeniowe, każdemu $x\in X$  przyporządkowujemy stan jego konta";
  • tabelką, np.:

  • grafem, jak wyżej;
  • wzorem analitycznym, np.: f:R$\rightarrow$[0, $\infty$), f(x)=x2;
  • funkcje o dziedzinie będącej podzbiorem zbioru liczb rzeczywistych można zinterpretować jako zbiór punktów płaszczyzny i przedstawić na rysunku zwanym wykresem funkcji; dla przykładu prezentujemy wykres dla funkcji z poprzedniego podpunktu:

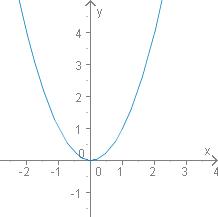
Przykłady:

  • przyporządkowanie każdemu psu liczby jego pcheł (w danej chwili);
  • przyporządkowanie każdemu uczniowi jego numeru w dzienniku;
  • każdej liczbie rzeczywistej przyporządkowujemy jej kwadrat;
  • $f:(0,\infty) \rightarrow$R, $f(x)=\sqrt{x}$ ;
  • +:R$\times$R$\rightarrow$R, +(p,q)=p+q.

Kontrprzykłady:

 

Rodzaje funkcji:

Własności:

  •  funkcję f:X$\rightarrow$Y nazwiemy różnowartościową (injekcją) dokładnie wtedy, gdy każdemu argumentowi  przyporządkowuje ona inną wartość, czyli:  $\forall x_1 , x_2 \in X \; (f( x_1 ) = f( x_2 ) \Rightarrow x_1 = x_2 )$;
  • funkcję f:X$\rightarrow$Y nazwiemy funkcją na zbiór Y (surjekcją) dokładnie wtedy, gdy każdy element przeciwdziedziny jest wartością pewnego argumentu, czyli: \forall y \in Y \; \existc x \in X (y=f(x));
  • funkcję nazwiemy wzajemnie jednoznaczną (bijekcją) dokładnie wtedy, gdy jest jednocześnie injekcją i surjekcją.

Monotoniczność funkcji:

Jeśli zbiory X i Y funkcji f:X$\rightarrow$Y są uporządkowane liniowo (czyli każde dwa elementy można ze sobą porównać), można przypisać funkcji następujące cechy:

  • funkcja jest rosnąca jeśli wraz ze wzrostem argumentów rosną ich wartości, czyli: $\forall x_1 , x_2 \in X , \; x_2 < x_1 \Rightarrow f(x_2) < f(x_1)$;
  • funkcja jest stała jeśli dla każdego argumentu wartość funkcji jest taka sama, czyli: $\forall x_1 , x_2 \in X , \; f(x_1) = f(x_2)$;
  • funkcja jest malejąca jeśli wraz ze wzrostem argumentów maleją ich wartości, czyli: $\forall x_1 , x_2 \in X , \; x_2 < x_1 \Rightarrow f(x_2) > f(x_1)$.

Funkcja okresowa:

Jeżeli dla funkcji $f:X\rightarrow$R (gdzie X to podzbiór liczb rzeczywistych R), istnieje liczba T$ > $0, zwana okresem funkcji, że dla każdego $x\in X$ jest $x+T\in X$ oraz $f(x) = f(x+T)$, to funkcję f nazywamy funkcją okresową.

Parzystość i nieparzystość funkcji:

Funkcja $f:X\rightarrow$R, (gdzie X jest symetrycznym względem zera podzbiorem zbioru liczb rzeczywistych R) jest funkcją parzystą, jeśli wykres funkcji f jest symetryczny względem osi rzędnych, czyli:
$\forall x \in X, \; f(-x)=f(x).$
Jeśli zaś wykres funkcji f jest symetryczny względem początku układu współrzędnych, czyli:
$\forall x \in X, \; f(-x)=-f(x).$
to tę funkcję nazwiemy funkcją nieparzystą.

Istnieją funkcje, które nie są ani parzyste, ani nieparzyste, np.: f:R$\rightarrow$R, f(x)=(x-1)2. Funkcja f:R$\rightarrow$R, f(x)=0 jest funkcją parzystą i nieparzystą jednocześnie.

Każdą
funkcję o wartościach rzeczywistych zdefiniowaną na symetrycznym
względem zera podzbiorze zbioru liczb rzeczywistych można przedstawić
jako sumę funkcji parzystej i funkcji nieparzystej.

 

Funkcja odwrotna:

Dla każdej bijektywnej funkcji f istnieje jedyna tak zwana funkcja odwrotna oznaczana f -1. Funkcja odwrotna do funkcji f:X$\rightarrow$Y odwzorowuje zbiór Y w zbiór X w taki sposób, że f -1(y)=x dokładnie wtedy, kiedy f(x)=y. Łatwo zauważy, że $( f^{-1} \circ f ) (x) = (f \circ f^{-1}) (x) =x$.

wykres symetryczny

 

elementarna, liniowa, wykładnicza, trygonometryczna

Działania na funkcjach:

Złożenie funkcji:

Jeżeli f:X$\rightarrow$Y oraz g:Y$\rightarrow$Z, to można zdefiniować funkcję $g\circ f, \; (g\circ f)(x)=g(f(x))$, zwaną złożeniem funkcji f i g.

 

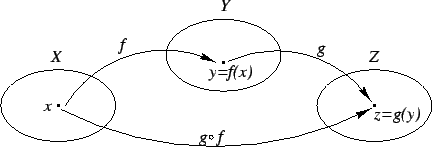
Obcięcie funkcji:

Każdą funkcję można ograniczyć do pewnego podzbioru jej dziedziny. Dla danej funkcji f:X$\rightarrow$Y oraz zbioru $Z$, obcięciem (ograniczeniem) funkcji f do zbioru Z nazywamy funkcję $f \mid Z : Z \rightarrow Y$ taką, że $(f \mid Z)(x) = f(x)$.

Przedłużenie funkcji:

Jeżeli $X\subset Z$ to przedłużeniem (rozszerzeniem) funkcji f:X$\rightarrow$Y do zbioru Z nazywamy każdą funkcję g:Z$\rightarrow$Y taką, że dla $x\in X$ zachodzi f(x)=g(x).

Obcięcie funkcji do danego podzioru dziedziny jest jedyne, natomiast przedłużenia funkcji do danego nadzbioru dziedziny zazwyczaj można dokonać na wiele sposobów.

Działania na funkcjach a przekształcenia wykresu funkcji:

 

Historia:

  • Pierwszą sformalizowaną na gruncie teorii mnogosci definicję funkcji podał Peano w 1905 roku. 

 

Terminy pokrewne:

  •  

 

‹ Fw góręK ›

Powrót na górę strony