Zad. 1. Dwa identyczne prostokąty ustawiono jak na rysunku. Czy kąt KOT może być ostry? Uzasadnij!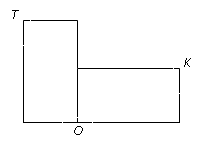 
Zad. 2. Wypisujemy liczby 1, 2, 4, 5, 6, ... - kolejne całkowite dodatnie, pomijając takie, które mają w swoim zapisie trójkę. Jaka będzie tysięczna wypisana liczba?
Zad. 3. Czy kwadrat da się podzielić na 1234567 kwadratów? Uzasadnij!
Ośmioro Ligowiczów z SP nadesłało w tym miesiącu w pełni poprawne rozwiązania zadań, otrzymując po 3 punkty. Byli to: Zuzanna Banaś, Marek Hajduk, Wiktor Koropczuk, Oliwia Kropidłowska, Ksymena Kukla, Zofia Ogonek, Barbara Turniak i Barbara Wachowicz. Natomiast po 2,5 punktu zdobyli: Jakub Dziedzic, Joanna Lisiowska i Bartosz Szczerba.
Najlepsze wyniki w Lidze Szkół Podstawowych w roku szkolnym 2012/13 osiągnęli:
- I m. (27 pkt na 27 możliwych) - Barbara Wachowicz (SP 13 w Chorzowie),
- II m. (26,5 pkt) - Barbara Turniak (SP 107 we Wrocławiu),
- III m. (26 pkt) - ex aequo: Marek Hajduk (SP 9 w Lubinie), Oliwia Kropidłowska (SP 76 we Wrocławiu), Ksymena Kukla (SP 13 w Chorzowie), i Joanna Lisiowska (Katolicka SP w Warszawie),
- IV m. (25 pkt) - ex aequo: Wiktor Koropczuk (SP 1 w Gorzowie Wielkopolskim) oraz Karolina Kalinowska i Paulina Pilat (obie z SP 107 we Wrocławiu),
- V m. (24,5 pkt) - ex aequo: Zuzanna Banaś (SP w Bielanach Wrocławskich) i Zofia Ogonek (SP 52 w Warszawie),
- VI m. (22,5 pkt) - Łukasz Czerwiec (SP 76 we Wrocławiu),
- VII m. (21 pkt) - Magdalena Owczarek (SP 35 w Legionowie),
- VIII m. (19 pkt) - ex aequo: Kacper Bernaciak (SP 30 we Wrocławiu) i Klaudia Pucek (ZSP w Smolcu),
- IX m. (18,5 pkt) - ex aequo: Mariusz Kądziela (SP w Uciechowie) i Konrad Wójcik (SP w Kozłowie,
- X m. (18 pkt) - Julia Pucek (ZSP w Smolcu).
Wszystkim serdecznie gratulujemy!
Zad. 1. Nie może - pionowy odcinek dzieli go na dwa kąty, z których można złożyć kąt przy wierzchołku prostokąta, jest to zatem zawsze kąt prosty.
Zad. 2. 1441: do 1400 pominiemy 200 liczb, które mają trójkę na miejscu setek, a z pozostałych 1200 liczb 10 w każdej setce ma trójkę jako cyfrę dziesiątek, a 9 innych trójkę na pozycji jedności, więc do 1400 wypisane będą 1200-19·12 = 972 liczby, a kolejnych 28 to 1401, 1402, 1403, ..., 1441 poza 1403, 1413, 1423 i 1430 do 1439.
Zad. 3. Kwadrat łatwo podzielić na 4 kwadraty. Jeśli dowolny z nich podzielimy też na 4 kwadraty, to oryginalny kwadrat będzie podzielony na 7 kwadratów. Jeśli którykolwiek z nich znów podzielimy na 4, liczba kwadratów znowu wzrośnie o 3 itd. - otrzymać możemy 4+3+3+3+...+3 kwadraty, gdzie liczba trójek jest dowolna. Ponieważ 1234567 daje przy dzieleniu przez 3 resztę 1, w pewnym kroku takiego postępowania, podzielimy wyjściowy kwadrat na 1234567 kwadratów. (Można to zresztą zrobić także na wiele innych sposobów).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
