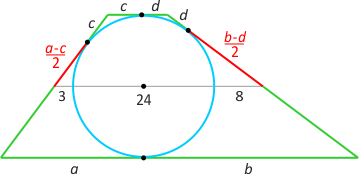
Zad. 1. Okrąg wpisany w trapez dzieli linię średnią na odcinki o długościach 3, 24 i 8. Oblicz długość większej podstawy.
Zad. 2. W trapez wpisano okrąg. Ramiona trapezu mają długości |AD|=21 i |BC|=24, a podstawa CD ma długość 9. Jakiej długości odcinek wycina okrąg z przekątnej AC?
Zad. 3. W trójkąt ABC wpisano okrąg, który dzieli środkową AM na trzy równe odcinki. Wiedząc, że |AC| = 5, oblicz długości pozostałych boków.
Zad. 4. (wolna amerykanka) W trójkącie ABC kąt C jest prosty, a |AC| = 1. Wiedząc, że kąt AIM jest prosty (gdzie I jest środkiem okręgu wpisanego w trójkąt, a M - środkiem boku AB), oblicz długość boku BC.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan),
- 22 - Radosław Górzyński (uczeń I LO Lubin).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Filip Derejski (student mechatroniki na AGH w Krakowie), Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Wprowadźmy oznaczenia jak na rysunku. Wówczas z twierdzenia o potędze punktu względem okręgu mamy ((a–c)/2)2 = 3·27 oraz ((b–c)/2)2 = 8·32, skąd otrzymujemy a–c = 18 i b–d = 32, a po dodaniu stronami otrzymamy (1) a+b–(c+d) = 50. Ze wzoru na długość linii średniej trapezu mamy (a+b+c+d)/2 = 35, skąd otrzymujemy (2) a+b+c+d = 70. Dodając teraz stronami (1) i (2), otrzymujemy a+b = 60.
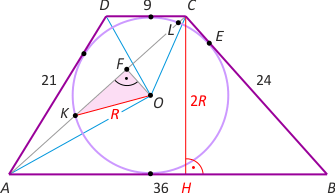
Zad. 2. Z warunku wpisywalności okręgu w czworokąt mamy |AB|+|CD| = |AD|+|BC|, skąd |AB| = 36. Mając dane długości czterech boków trapezu, łatwo obliczyć jego wysokość |CH| = 2R = 8√5, a potem przekątną |AC| = 12√5. Wystarczy teraz obliczyć długość OF. Zauważmy, że PAOC = PAOD + PDOC – PADC = |AD|·R/2 + |DC|·R/2 – |DC|·2R/2 = (R/2)·(21+9–18) = 24√5. Z drugiej strony PAOC = |AC|·|OF|/2 = |OF|·6√5, zatem |OF|=4. Z twierdzenia Pitagorasa w trójkącie KOF mamy |KF|= 8 i ostatecznie |KL|=16.
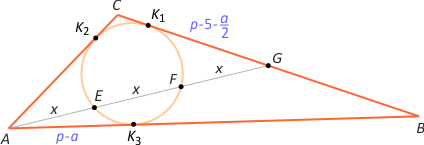
Zad. 3. Niech |BC|=a, a p jest połową obwodu trójkąta ABC. Wówczas |AK3|= p–a, |BK1|= p–5 oraz |BM|=a/2. Z twierdzenia o potędze punktu względem okręgu mamy (p–a)2 = 2x2 oraz (p–5–(a/2))2 = 2x2, skąd a=10. Dalej (p–10)2 = 2x2, skąd x = (p–10)/√2 = ((15+|AB|)/2)–10)/√2 = (|AB|–5)/(2√2). Wówczas |AM| = 3x =3·(|AB|–5)/(2√2). Korzystając ze wzoru na długość środkowej, po podstawieniu i przekształceniach otrzymujemy równanie 5|AB|2–90|AB|+325 = 0, skąd |AB|=13. Ostatecznie długości boków trójkąta wynoszą 5, 10 i 13.
Intencją autora zadania było rozpatrzenie przypadku gdy p–5–(a/2) >0, a tym samym |AB|>5. Chwała tym, którzy podali dodatkowe rozwiązanie 5, 25/13 i 50/13.
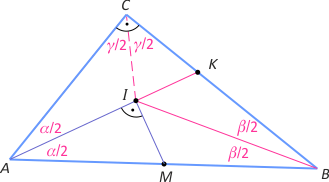
Zad. 4. (wolna amerykanka) Przedłużmy odcinek AI do punktu K. Łatwo zauważyć, że |∡AIB| = 135° oraz |∡MIB|=|∡BIK|=45°. Wynika stąd przystawanie trójkątów MIB oraz BIK (cecha kbk), przy czym |MB|=|BK|. Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy 1:|AB| = |CK|:|BK| = |CK|:1/2|AB|, skąd |CK|=1/2. Z twierdzenia Pitagorasa dla trójkąta ABC otrzymujemy |BK|=5/6 i ostatecznie |BC|=4/3.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
