grudzień 2023

grudzień 2023

Data ostatniej modyfikacji:
2024-07-6

Zad. 1. Bartek rozsypał na stole 10 kostek do gry, a następnie obliczył sumę wszystkich oczek na ściankach, które mógł zobaczyć, nie przewracając kostki. Wynik wyniósł 186. Ile co najwyżej szóstek mogło być na niewidocznych ściankach?

Zad. 2. Na spotkanie stada gęsi wyleciał gąsior i woła: „Witajcie sto gęsi”. Na to lecąca na przedzie gęś odpowiedziała: „W naszym stadzie nie ma stu gęsi. Ale gdyby było nas jeszcze raz tyle, i jeszcze połowa i jeszcze ćwierć naszego stada, i jeszcze ty razem z nami, to wtedy byłoby sto gęsi". Ile gęsi leciało w tym stadzie?

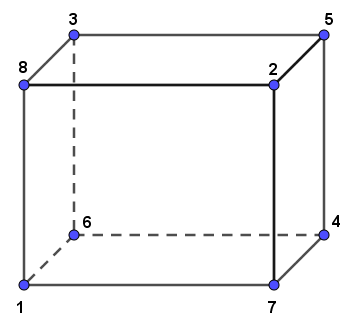
Zad. 3. Czy można ponumerować wierzchołki sześcianu liczbami od 1 do 8 tak, aby sumy numerów wierzchołków z każdej ściany były równe? Odpowiedź uzasadnij.

Wyniki:

W grudniu punkty zdobyli:

3 – Maja Bator SP 44 Wrocław, Florian Bialas SP 3 Dobrzeń Wielki, Krzysztof Bednarz SP Głogów Małopolski, Aleksandra Besuch SP 64 Wrocław, Paulina Błasiak SP Długołęka, Maria Bogner SP Fundacji Królowej Św. Jadwigi Wrocław, Mieszko Buczkowski SP 2 Ożarów Mazowiecki, Natalia Bulak SP 3 Śinawa, Emilia Burkovtseva SP 44 Wrocław, Wiktor Bychowiec SP 16 Wrocław, Igor Bychowiec SP 16 Wrocław, Piotr Celiński SP Fundacji Królowej Świętej Jadwigi, Arseniia Elkina SP 16 Wrocław, Michał Filipczak SP 44 Wrocław, Agata Fudała SP 53 Wrocław, Anna Gil SP 44 Wrocław, Jakub Gil SP 44 Wrocław, Stanisław Hajgiel SP STO Warszawa, Gabriela Jaśkowska SP Płomień Katowice, Damian Jaromin SP 44 Wrocław, Mateusz Jaszczyszyn SP 44 Wrocław, Claudia Jończyk SP Jedlnia-Letnisko, Nadia Liszka SP 5 Myszków, Gabriela Kapica SP Strzelce, Daria Karnitskaya SP 107 Wrocław, Wojciech Kasprzyk SP 4 Wieliczka, Filip Kaźmierczak SP 44 Wrocław, Tomasz Kisielewski SP 50 Wrocław, Szymon Kmiotek SP 15 Kraków, Laura Konieczna SP 2 Plewiska, Adam Kosarzycki SP 16 Wrocław, Eryk Kwapisz SP 44 Wrocław, Natan Łazarewicz Szkoła w Chmurze, Anastazja Marciniak SP 3 Mogilno, Miron Możdżyński SP 20 warszawa, Dawid Niklewicz SP 44 Wrocław, Mateusz Noga SP 113 Wrocław, Małgorzata Nowakowska SP 3 Głogów, Milena Orska SP 16 Wrocław, Borys Osieczko SP 8 Sopot, Adam Pająk SP Raszyn, Antonina Pawliszyszyn SP Płomień Katowice, Leon Płonka SP 44 Wrocław, Nina Pociecha SP 100 Warszawa, Dagmara Skulimowska SP 50 Wrocław, Zuzanna Skulimowska SP 50 Wrocław, Stanisław Solski SP 13 Zielona Góra, Witold Stępień SP 1 Oleśnica, Lena Szkirpan SP 50 Wrocław, Adam Trznadel SP 82 Wrocław, Kalina Tułacz SP 50 Wrocław, Amelia Waindok SP 3 Dobrzeń Wielki, Lena Wałazińska SP 221 Warszawa, Julian Wawer SP Pilawa, Franciszek Węgrzyn SP 44 Wrocław, Zuzanna Winiarska SP 44 Wrocław, Ignacy Włodarski SP 36 Wrocław, Kacper Wołowiec SP 50 Wrocław, Hanna Wójcik SP 50 Wrocław, Filip Zawłocki SP 100 Warszawa;
2 – Jakub Derewecki SP 50 Wrocław, Adam Gajdzis SP 107 Wrocław, Aleksander Gajdzis SP 107 Wrocław, Stanisław Góralski SP Józefów n. Wisłą, Hanna Górska SP Długołęka, Luiza Gruchalski SP Dobrzeń Wielki, Hanna Janiec SP Kostomłoty, Karolina Grzyb SP Płomień Katowice, Julia Kalinowska SP Długołęka, Kurt Kolodii SP 44 Wrocław, Szymon Kołodziejczyk SP Józefów n. Wisłą, Misza Lahuta SP 44 Wrocław, Amelia Marciniak SP 3 Mogilno,Tymoteusz Libawski SP Dobrzeń Wielki, Julia Pawlińska SP Józefów n. Wisłą, Antonina Pawliszyszyn SP Płomień Katowice, Jakub Ptak SP 22 Wrocław, Marek Raszczyk SP Zawada, Mateusz Różalski SP Józefów n. Wisłą, Dawid Rydzik SP 60 Kraków, Maja Samsel SP 26 Kraków, Filip Staszkiewicz SP 50 Wrocław Krzysztof Szymanowski SP 50 Wrocław, Maria Święs SP 60 Kraków, Kajetan Uramek SP 82 Wrocław, Liwia Wer SP Dobrzeń Wielki, Jakub Wojciechowski SP 44 Wrocław, Dawid Zysk SP 19 Legnica;
1 – Mykhailo Anufriyev SP 16 Wrocław, Weronika Grzyb SP Płomień Katowice, Paweł Jarzyński SP 13 Zielona Góra, Amelia Łakomiec SP 50 Wrocław, Wojciech Ożóg SP Długołęka, Damian Ryś SP 16 Wrocław, Zofia Weber SP Płomień Katowice.

Pozostali uczestnicy otrzymali poniżej 1 punktu.

Odpowiedzi:

Zad. 1. Suma oczek na kostce wynosi 1+2+3+4+5+6 = 21. Suma oczek na 10 kostkach wynosi 10·21 = 210, zatem suma oczek na niewidocznych ściankach to 210–186 = 24. Szóstek mogłoby być 24:6 = 4, ale wtedy na pozostałych kostkach byłoby zero oczek, co jest niemożliwe. Gdyby były 3 szóstki, to suma oczek na pozostałych 7 kostkach wynosiłaby 6, czyli na jednej kostce byłoby zero oczek. Zatem szóstki na niewidocznych ścianach mogły być co najwyżej dwie.

Zad. 2. Oznaczmy przez x liczbę gęsi. Na podstawie warunków zadania otrzymujemy x+x+¹/₂x+¹/₄x+1 = 100, skąd x=36. W stadzie leciało 36 gęsi.

Zad. 3. Suma numerów wierzchołków na każdej ścianie wynosi 18.