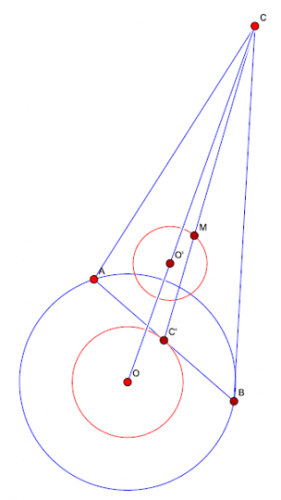
Zad. 1. Punkty A i B leżą na okręgu, a punkt C na zewnątrz tego okręgu. Niech punkt M będzie środkiem ciężkości trójkąta ABC. Jaką figurę zakreśli punkt M, jeżeli punkty A i B będą poruszały się po okręgu zachowując na nim początkową odległość?
Zad. 2. Dany jest trójkąt równoboczny ABC o boku długości a. Łączymy odcinkami środki A1, B1, C1 boków tego trójkąta, a otrzymany w ten sposób trójkąt zamalowujemy. W drugim kroku, w każdy z trzech niezamalowanych trójkątów AB1C1, A1BC1, A1B1C wpisujemy nowe trójkąty, łącząc środki boków, a otrzymane trójkąty wpisane zamalowujemy. W każdym następnym kroku postępujemy analogicznie - w trójkąty niezamalowane wpisujemy nowe trójkąty, zamalowując je. Oblicz sumę pól i sumę obwodów zamalowanych trójkątów po n krokach.
Zad. 3 Jakie jest największe możliwe pole prostokąta, którego wierzchołki leżą na bokach trójkąta równobocznego o boku długości a?
W grudniu punkty zdobyli:
- 3 – Michał Węgrzyn ALO PWr Wrocław;
- 2,5 – Zuzanna Czapiewska ZSB Słupsk, Radosław Górzyński I LO Lubin, Joanna Nowakowska LO Aslan Głogów, Cezary Rębiś ZS Elektronicznych Radom, Julia Śnieżek I LO Nysa;
- 2 – Emilia Cichowska II LO Lubin, Miłosz Zakrzewski LO Tuchola;
- 1,5 – Artur Bumażnik ZS Elektronicznych Jelenia Góra, Aleksander Kiszkowiak I Technikum Elektroniczne Warszawa;
- 1 – Filip Kleczewski I LO Głubczyce.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Oznaczmy środek okręgu, po którym poruszają się punkty A i B, przez O. Środek C’ odcinka AB zakreśli okrąg o środku w punkcie O. Środek ciężkości trójkąta ABC jest obrazem punktu C’ w jednokładności o środku w punkcie C i skali 2:3. Punk M porusza się zatem po okręgu o środku leżącym w 2/3 odcinka CO o promieniu długości 2/3|OC’|.
Zad. 2. Łącząc środki boków trójkąta, w kolejnych krokach otrzymujemy trójkąty podobne o bokach dwa razy mniejszych. Pola tych trójkątów wynoszą odpowiednio [tex]P_1=\frac{(\frac{a}{2})^2\sqrt{3}}{4}, P_2=\frac{(\frac{a}{2^2})^2\sqrt{3}}{4}, P_3=\frac{(\frac{a}{2^3})^2\sqrt{3}}{4}, ..., P_n=\frac{(\frac{a}{2^n})^2\sqrt{3}}{4}[/tex]. Liczba jednakowych trójkątów za każdym razem potraja się, zatem suma pól jednakowych trójkątów wynosi kolejno S1=P1, S2=3P2, S3=32P3, ..., Sn=3n-1Pn, czyli [tex]S_1=\frac{(\frac{a}{2})^2\sqrt{3}}{4}, S_2=3\cdot\frac{(\frac{a}{2^2})^2\sqrt{3}}{4}, S_3=3^2\cdot\frac{(\frac{a}{2^3})^2\sqrt{3}}{4}, ..., S_n=3^{n-1}\cdot\frac{(\frac{a}{2^n})^2\sqrt{3}}{4}[/tex]. Otrzymaliśmy ciąg geometryczny o ilorazie [tex]\frac{S_{n+1}}{S_n}=\frac{3^n\cdot\frac{(\frac{a}{2^{n+}})^2\sqrt{3}}{4} }{3^{n-1}\cdot\frac{(\frac{a}{2^n})^2\sqrt{3}}{4}}=\frac{3}{4}[/tex]. Suma n początkowych wyrazów ciągu wynosi P1+3P2+32P3+…+3n-1Pn=[tex] \frac{(\frac{a}{2})^2\sqrt{3}}{4}\cdot\frac{1-(\frac{3}{4})^2}{1-\frac{3}{4}}=\frac{a^2\sqrt{3}}{4}\cdot(1-(\frac{3}{4})^n) [/tex].
Sumy obwodów jednakowych trójkątów wynoszą odpowiednio [tex] O_1=3\cdot\frac{a}{2}, O_2=3^2\cdot\frac{a}{2^2}, O_3=3^3\cdot\frac{a}{2^3}, …, O_n=3^n\cdot\frac{a}{2^n}[/tex]. Jest to ciąg geometryczny o ilorazie [tex]\frac{O_{n+1}}{O_n}=\frac{3^{n+1}\cdot\frac{a}{2^{n+1}}}{3^n\cdot\frac{a}{2^n}}=\frac{3}{2}[/tex]. Suma n początkowych wyrazów tego ciągu wynosi [tex]=O_n=\frac{3}{2}a\cdot\frac{1-(\frac{3}{2})^n}{1-\frac{3}{2}}=3a\cdot((\frac{3}{2})^n-1) [/tex].

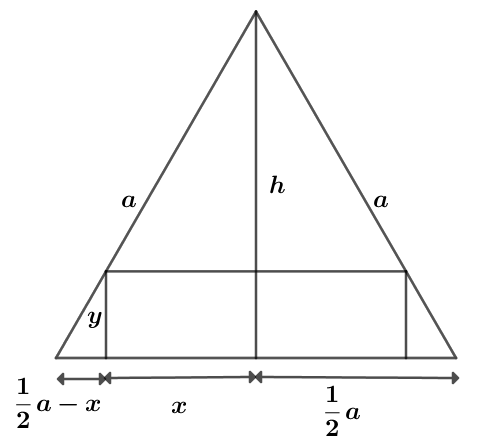
Zad. 3. Na podstawie podobieństwa trójkątów (cecha kkk), otrzymujemy proporcję [tex] \frac{h}{\frac{1}{2}a}=\frac{y}{\frac{1}{2}a-x}[/tex], skąd [tex] y=-\sqrt{3}x+\frac{1}{2}\sqrt{3}a[/tex]. Pole prostokąta wynosi P = 2xy, czyli [tex] P=-2\sqrt{3}x^2+a\sqrt{3}x[/tex]. Jest to funkcja kwadratowa, której wykresem jest parabola o ramionach skierowanych w dół, zatem funkcja osiąga maksimum [tex]P_{max}=\frac{-3a^2}{4\cdot-2\sqrt{3}}=\frac{a^2\sqrt{3}}{8}[/tex].






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 

