Zad.1. Czy można ponumerować krawędzie czworościanu liczbami od 1 do 6 tak, aby sumy numerów krawędzi z każdej ściany były równe? Odpowiedź uzasadnij.
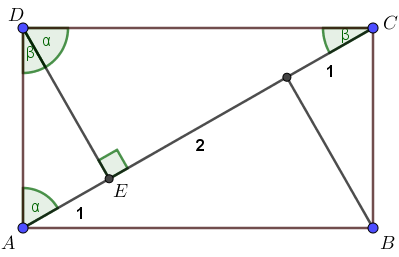
Zad. 2. Przez przeciwległe wierzchołki prostokąta poprowadzono proste prostopadłe do przekątnej łączacej pozostałe dwa wierzchołki. Podzieliły one tę przekątną na odcinki o długości 1 cm, 2 cm i 1 cm. Oblicz długości boków tego prostokąta.
Zad. 3. Ustaw w porządku rosnącym liczby 960, 3160, 560, 2750, 2240. Odpowiedź uzasadnij, nie obliczając tych liczb.
W grudniu punkty zdobyli:
- 3 – Natalia Czurejno SP Wykroty, Antoni Grębowiec SP 44 Wrocław, Aleksander Masztalski SP 3 Mikołów, Szymon Michalik SP 3 Przymierza Rodzin Warszawa, Gabriela Pułecka SP 2 Brzeg Dolny, Yaraslau Sialiuk SP 82 Wrocław, Wiktor Szwarczyński SP Szkoła w chmurze Poznań;
- 2 – Eliza Banaszkiewicz SP Strzelce, Anna Frankowska SP 139 Warszawa, Ewa Nowakowska SP Strzelce, Karolina Piątkowska SP 16 Wrocław, Aleksandra Pniaczek SP 50 Wrocław;
- 1,5 – Alicja Picińska SP 64 Wrocław, Jan Węgrzyn SP 44 Wrocław;
- 1 – Hanna Kleczkowska Eropejska SP Kraków, Julia Strzelecka SP 50 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Każda krawędź czworościanu należy do dwóch ścian, zatem suma numerów krawędzi wszystkich ścian wynosi 2·(1+2+3+4+5+6) = 42. Liczba 42 nie jest podzielna przez 4, zatem nie można ponumerować krawędzi czworościanu liczbami od 1 do 6 tak, aby sumy numerów krawędzi z każdej ściany były równe.
Zad. 2. Przekątna dzieli prostokąt na dwa przystające trójkąty prostokątne o kątach α, β, 90°. Proste prostopadłe podzieliły każdy z trójkątów na dwa trójkąty podobne. Z podobieństwa trójkątów AED i DCE otrzymujemy proporcję |DE|:1 = 3:|DE|, skąd |DE|=√3. Na podstawie twierdzenia Pitagorasa otrzymujemy dwa równania |AD|2 = 12+√32 i |DC|2 = 32+√32, skąd |AD|=2 cm i |DC|=2√3.
Zad. 3. Zachodzi 560 < 960. Liczby 960, 3160 i 2750 przedstawiamy w postaci potęg liczby 3. Mamy 960 = (32)60 = 3120, 2750 = (33)50 = 3150, zatem 560 < 960< 2750< 3160. Pozostaje do ustalenia, na którym miejscu jest liczba 2240. Przedstawmy teraz liczby 2750 i 2240 w postaci potęg o wykładniku 30 oraz liczby 3160 i 2240 w postaci potęg o wykładniku 80. Mamy 2750 = ((33)5)10= (35)30 = 24330 i 2240 = (28)30 = 25630 oraz 3160 = (32)80 = 980 i 2240 = (23)80 = 880, czyli 2750<2240 i 2240<3160. Ostatecznie otrzymujemy 560 < 960< 2750 < 2240< 3160.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
