Zad. 1. Grupa cyklistów wybrała się na wycieczkę rowerową. Wyruszyli w środę po południu, a jechali aż do Piątku, chociaż cała wyprawa trwała tylko niecałą dobę (z noclegiem po drodze). Jak to możliwe?
Zad. 2. Pewne państwo położone jest na trzech wyspach. Mieszkańcy wyspy A są prawdomówni, mieszkańcy wyspy B to notoryczne kłamczuchy, a mieszkańcy wyspy C mają dziwny zwyczaj: od urodzenia na zmianę kłamią i mówią prawdę. Z jednym z wyspiarzy przeprowadzono krótki wywiad:
- Skąd Pan pochodzi?
- Z wyspy C.
- A która z Waszych wysp jest najmniej zaludniona?
- B.
Czy wiadomo, czy ankietowany powiedział prawdę? Na jakiej podstawie?
Zad. 3. Na pewnej konferencji naukowej spotkali się profesorowie Schmidt, Ferrari, Kovács i Kuzniecow. Rozmawiając ze sobą, używają tylko niemieckiego, włoskiego, węgierskiego i rosyjskiego. Niemiec, prof. Schmidt nie mówi po włosku, ale odgrywa rolę tłumacza, gdy Włoch, prof. Ferrari chce się porozumieć z prof. Kovácsem. Pochodzący z Budapesztu prof. Kovács swobodnie porozumiewa się z prof. Kuzniecowem, chociaż ten nie potrafi powiedzieć ani zdania po węgiersku. W trakcie obrad profesorowie zauważyli, że Schmidt, Ferrari i Kuzniecow nie są w stanie rozmawiać w trójkę w jednym języku, ale każdy z czterech profesorów zna dwa spośród używanych przez nich w rozmowach języków, chociaż nikt nie zna jednocześnie niemieckiego i węgierskiego. Który profesor włada jakimi językami?
Wszystkie lutowe zadania poprawnie rozwiązali: Paulina Witasik z SP 99 we Wrocławiu, Łukasz Kajdan z SP 82 w Poznaniu, Michalina Sieradzka z G 49 we Wrocławiu, Konrad Konarski z I LO w Legnicy, Andrzej Kunca nauczyciel matematyki z Gostycyna, Damian Olczyk z I LO w Oleśnie, Krystyna Lisiowska redaktor techniczny z Warszawy, Dariusz Trzeciak nauczyciel TI z Zambrowa.
Poprawne rozwiązania 2 zadań przysłali: Dominika Dąbrowska z SP 99 we Wrocławiu, Stella Kielan z SP 99 we Wrocławiu, Katarzyna Zając z SP 99 we Wrocławiu, Agata Grzelczak z G 3 w Głogowie, Ilona Kopeć z II LO w Legnicy, Jonatan Stokłosa z I LO w Legnicy.
Gratulujemy!
W klasyfikacji generalnej prowadzą (na 15 możliwych pkt.): Damian Olczyk z I LO w Oleśnie (15 pkt.), Łukasz Kajdan z SP 82 w Poznaniu (14 pkt.), Michalina Sieradzka z G 49 we Wrocławiu (12 pkt.), Krystyna Lisiowska redaktor techniczny z Warszawy (12 pkt.), Dariusz Trzeciak nauczyciel TI z Zambrowa (12 pkt.), Dominika Dąbrowska z SP 99 we Wrocławiu (11 pkt.), Stella Kielan z SP 99 we Wrocławiu (11 pkt.), Konrad Konarski z I LO w Legnicy (11 pkt.), Andrzej Kunca nauczyciel matematyki z Gostycyna (11 pkt.), Paulina Witasik z SP 99 we Wrocławiu (9 pkt.).
Zad. 1. Jechali do Piątku w województwie łódzkim (i dojechali w czwartek).
Zad. 2. Ankietowany nie mógł pochodzić z A, bo wówczas na pierwsze pytanie odpowiedziałby "z A". Gdyby pochodził z B, skłamałby, odpowiadając na oba pytania, gdyby był zaś z C, oznaczałoby to, że na pierwsze pytanie odpowiedział prawdziwie, więc skłamał, odpowiadając na drugie. Na pewno zatem nieprawdą jest, jakoby najmniej zaludnioną wyspą była B.
Zad. 3. Dane zadania można zapisać w tabelce: 
(każdy profesor mówi w swoim ojczystym języku, Schmidt nie mówi po włosku, Kuzniecow po węgiersku, nikt nie zna węgierskiego i niemieckiego, każdy zna dwa języki, Schmidt, Ferrari i Kuzniecow nie znają wspólnego języka). Ponieważ Schmidt tłumaczy rozmowy profesora Ferrari z profesorem Kovácsem, Ferrari musi znać niemiecki, a Kovács rosyjski. Jednocześnie wiadomo, że każdy zna po dwa języki, a jednocześnie Schmidt, Ferrari i Kuzniecow nie mogą mieć plusów wszyscy w tym samym wierszu. Stąd wypełniamy już całą tabelkę: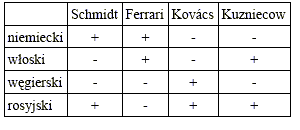 
i łatwo sprawdzić, że taki układ znajomości języków przez profesorów spełnia warunki zadania.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
