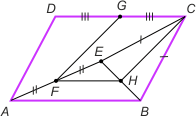
Zad. 1. Wewnątrz równoległoboku ABCD zaznaczmy punkt E taki, że |CB| = |CE|. Wykaż, że prosta BE jest prostopadła do prostej przechodzącej przez środki odcinków AE i DC.
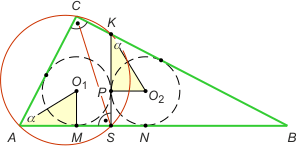
Zad. 2. Wewnątrz trójkąta prostokątnego dane są dwa styczne zewnętrznie okręgi o jednakowym promieniu. Oba są styczne do przeciwprostokątnej i do jednej z przyprostokątnych. Niech M i N będą punktami styczności na przeciwprostokątnej. Wykaż, że środek odcinka MN leży na dwusiecznej kąta prostego.
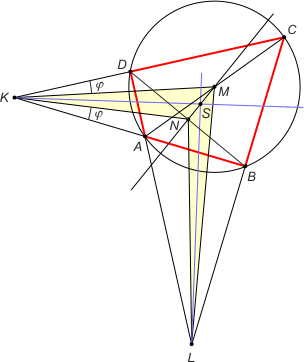
Zad. 3. Czworokąt ABCD jest wpisany w okrąg. Przedłużenia boków AB i CD przecinają się w punkcie K, a boków BC i AD - w punkcie L. Wykaż, że dwusieczne kątów BKC i BLA przecinają się na prostej przechodzącej przez środki odcinków AC i BD.
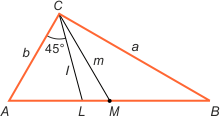
Zad. 4. (wolna amerykanka) W trójkącie prostokątnym ABC z wierzchołka kąta prostego poprowadzono środkową CM o długości m oraz dwusieczną CL o długości l. Oblicz pole tego trójkąta.
Maksymalną liczbę (30 pkt.) za zadania 1-3 zdobyli: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Mateusz Klein (uczeń, III LO Gdynia) ), Sławomir Matysiak (nauczyciel, LO Trzebnica), Michel Migas (student, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń) oraz Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca nr 131 Charków, Ukraina).
Maksymalną liczbę (10 pkt.) za zadanie 4 otrzymali: Jacek Bagiński, Włodzimierz Bąk, Mateusz Klein, Michel Migas, Tadeusz Porzucek, Sabina Khady Sy (studentka, UJ), Mikołaj Szamajew oraz Wojciech Tomiczek (inżynier, Lipowa).
Najważniejsza jest oczywiście przyjemność z rozwiązywania zadań, ale dla formalności przedstawiamy czołówkę Ligi po pięciu miesiącach (w nawiasach podajemy punkty z ligi geometrycznej i wolnej amerykanki): Włodzimierz Bąk (150, 50), Mateusz Klein (150, 50), Michel Migas (150, 50), Tadeusz Porzucek (150, 48), Jacek Bagiński, (140, 50), Iwona Gruszecka (140), Zygmunt Krawczyk (122, 50), Mikołaj Szamajew (118, 38), Sabina Sy(108, 50), Jakub Gajdecki (98, 40).
Gratulujemy!
Zad. 1. Niech F, G i H będą środkami odcinków AE, DC i EB. Zauważmy, że odcinek FH jest równoległy do AB i dwa razy od niego krótszy, bo jest linią średnią w trójkącie ABE. Oznacza to, że czworokąt FHCG jest równoległobokiem. Z drugiej strony odcinek CH jest środkową w trójkącie równoramiennym BCE, więc jest jednocześnie wysokością. Stąd teza.
Zad. 2. Niech SK będzie wspólną styczną do obu okręgów. Zauważmy, że na czworokącie ASKC można opisać okrąg (suma kątów S i C wynosi 180°). Wystarczy zatem wykazać, że |AS| = |SK|. Rozważmy trójkąty AMO1 oraz KPO2. Są one przystające na mocy cechy kbk (kąt prosty, promień okręgu wpisanego, połowa kąta α). Zatem |KP| = |AM| i dalej |AS| = |SK| jako sumy jednakowych odcinków, bo |MS| = |SP| = r.
Zad. 3. Niech M i N oznaczają środki odcinków AC i BD odpowiednio, a S jest punktem przecięcia dwusiecznej kąta BKC z prostą MN. Z podobieństwa trójkątów KAC i BKD (cecha kk - wspólny kąt K, kąty KCA i KBD oparte na łuku AD) wynika, że kąty BKN i CKM są przystające. Oznacza to, że KS jest dwusieczną kąta NKM i dzieli odcinek MN w stosunku |MS|/|SN| = |MK|/|NK| (z twierdzenia o dwusiecznej kąta wewnętrznego w trójkącie). Z podobieństwa trójkątów KAC i BKD mamy |MK|/|NK| = |AC|/|BD|. Analogicznie rozumując, otrzymujemy, że dwusieczna kąta BLA jest dwusieczną kąta MLN i dzieli odcinek w tym samym stosunku |AC|/|BD|. Stąd teza.
Zad. 4. Zauważmy, że środkowa opuszczona z wierzchołka kąta prostego jest dwa razy krótsza od przeciwprostokątnej (bo jest promieniem okręgu opisanego na trójkącie, a przeciwprostokątna jest jego średnicą). Stąd |AB| = 2m. Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy |AL|/|LB| = |AC|/|BC| = b/a. Stąd wynika, że a|AL| = b(2m–|AL|), czyli |AL| = 2mb/(a+b). Analogicznie |LB| = 2ma/(a+b). Korzystając ze wzoru Lagrange'a na długość dwusiecznej |CL|2 = |AC|·|CB| – |AL|·|LB| (patrz wyprowadzenie poniżej), otrzymujemy równanie l2 = ab – (2mb/(a+b))·(2ma/(a+b)). Dodatkowo z twierdzenia Pitagorasa mamy a2 + b2 = 4m2. Rozwiązując ten układ równań ze względu na ab/2 i podstawiając S = ab/2, otrzymujemy równanie 2S2 – l2S – l2m2 = 0, spełnione przez S = (l2 +l√(l2 + 8m2))/4.
Wzór Lagrange'a na długość dwusiecznej
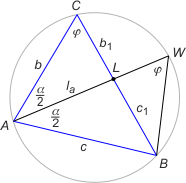
W trójkącie ABC odcinek dwusiecznej kąta A zawarty we wnętrzu trójkąta ma długość
la = √(bc–b1c1), gdzie b=|AC|, c=|AB|, b1=|BL|, c1=|LC| a L jest spodkiem dwusiecznej la kąta A (patrz rysunek poniżej).
Dowód
Wpiszmy trójkąt ABC w okrąg i niech W będzie punktem wspólnym tego okręgu i dwusiecznej kąta A. Z twierdzenia o cięciwach
okręgu mamy (1) |AL|·|LW| = |BL|·|LC|. Zauważmy, że trójkąty ALC oraz ABW są podobne (mają kąt α/2 i kąt wpisany oparty na łuku AB), skąd otrzymujemy |AL|/b = c/|AW| i równoważnie (2) |AL|·|AW| = bc. Podstawiając w (1) |LW| = |AW|–|AL|, otrzymujemy |AL|·(|AW|–|AL|) = |CL|·|LB|, skąd |AL|2 = |AL|·|AW|–|BL|·|LC|. Podstawiając z (2) i stosując początkowe oznaczenia, otrzymujemy wzór Lagrange'a.
Prawdziwy także jest inny wzór
la = 2bc·cos(α/2)/(b+c)
Dowód
Wyprowadzamy go przez sumowanie pól trójkątów składowych PABC = PABL + PALC, czyli 1/2 b·c·sinα = 1/2 a·la·sin(α/2) + 1/2 b·la·sin(α/2), co ze wzoru na sinus podwojonego kąta daje bcsin(α/2)cos(α/2) = 1/2 lasin(α/2)·(b+c), skąd otrzymujemy tezę.
Stosując drugi z podanych wzorów, w rozwiązaniu zadania 4 otrzymamy układ równań a2 + b2 = 4m2 oraz l = (ab√2)/(a+b). Korzystając ze wzoru skróconego mnożenia, otrzymujemy z pierwszego z równań 4m2 = (a+b)2 - 2ab, skąd a+b = √(4m2 + 2ab). Podstawiając to do drugiego równania i oznaczając ab/2 = S, otrzymujemy 2S2 – l2S – m2l2 = 0, jak poprzednio.
