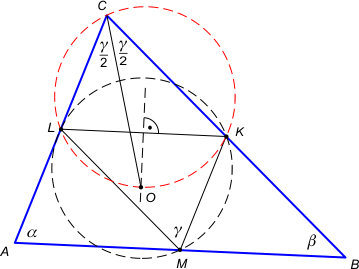
Zad. 1. Znajdź miarę kąta C w trójkącie różnobocznym ABC, wiedząc, że na jego dwusiecznej leży środek okręgu opisanego na trójkącie, którego wierzchołkami są środki boków wyjściowego trójkąta.
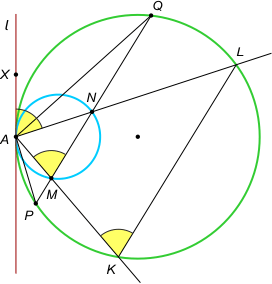
Zad. 2. Dwa okręgi są styczne wewnętrznie w punkcie A. Punkty P i Q leżą na większym okręgu, a punkty M i N są punktami przecięcia się prostej PQ z mniejszym okręgiem. Wykaż,
że kąty PAM i NAQ są przystające.
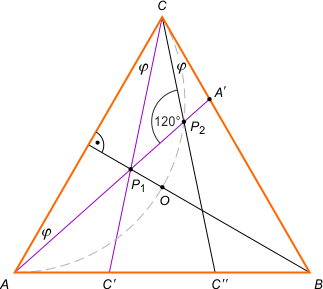
Zad. 3. Wewnątrz trójkąta równobocznego ABC obrano punkt P. Niech A' jest punktem wspólnym prostej AP i boku BC, a C' - punktem wspólnym prostej CP z bokiem AB. Znajdź zbiór wszystkich punktów P, dla których |AA'| = |CC'|.
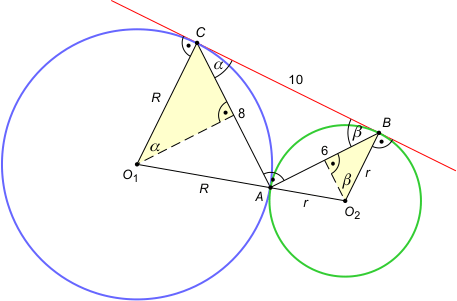
Zad. 4. (wolna amerykanka) Dwa okręgi są styczne zewnętrznie w punkcie A. Znajdź promienie tych okręgów, wiedząc, że cięciwy łączące punkt A z punktami styczności okręgów ze wspólną styczną zewnętrzną mają długości 6 i 8.
Za rozwiązania zadań 1-3 punkty zdobyli:
- 30 - Robert Ciężabka (student AGH Kraków ), Michel Migas (student PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Paweł Wesołowski (uczeń II LO Końskie) oraz Szymon Kaźmierowski (nauczyciel, IV LO Elbląg),
- 22 - Mikołaj Sikora (uczeń III LO Tarnów),
- 20 - Sabina Khady Sy (studentka UJ).
Za zadanie 4 maksymalną liczbe 10 pkt. otrzymali: Robert Ciężabka, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Sabina Khady Sy, Szymon Kaźmierowski oraz Wojciech Tomiczek (inżynier, Lipowa).
W XV Mistrzostwach Polski w Geometrii Elementarnej rozegranych 3 VI we Wrocławiu wzięli udział niektórzy uczestnicy Ligi Zadaniowej. W gronie laureatów znalazł się Mikołaj Sikora (IV m). Bardzo dobre wyniki uzyskali również: Michał Ciurej, Sławomir Matysik i Robert Ciężabka. Gratulujemy!
Zad. 1. W dowolnym trójkącie dwusieczna kąta i symetralna przeciwległego boku przecinają się w punkcie leżącym na okręgu opisanym (obie te proste dzielą odpowiedni łuk okręgu na połowy). Wynika stąd, że środek O, okręgu opisanego na trójkącie KLM, leży na okręgu opisanym na trójkącie LKC. Z założenia wiemy, że |∡LMK| = |∡C| = γ. Zatem |∡LOK| = 2γ, bo jest to kąt środkowy oparty na tym samym łuku. Ponieważ czworokąt LOKC jest wpisany w okrąg, mamy γ+2γ = 180°, a stąd γ = 60°.
Zad. 2. Poprowadźmy wspólną styczną do obu okręgów i przedłużmy odcinki AM i AN do przecięcia się z większym okręgiem w punktach K i L. Wystarczy pokazać, że prosta KL jest równoległa do PQ. Jest tak, bo kąty AMN i AKL są przystające (równe kątowi dopisanemu XAL). Wówczas równość miar kątów QAN i PAM wynika z równości miar kątów QAL i PAK opartych na przystających łukach.
Zad. 3. Obierzmy na boku BC dowolny punkt A'. Łatwo zauważyć, że na boku AB są dwa punkty C' i C" spełniające warunki zadania. Oznaczmy punkty przecięcia prostych CC' i CC" z odcinkiem AA' odpowiednio przez P1 i P2. Zauważmy, że P1 leży na wysokości opuszczonej z wierzchołka B. Z drugiej strony rozważając sumę kątów w trójkącie AP2C, można obliczyć, że |∡AP2C| = 120°. Oznacza to, że punkt P2 leży na łuku okręgu przechodzącego przez punkty A i C oraz środek okręgu opisanego na trójkącie ABC.
Zad. 4. (wolna amerykanka) Kąty BCA i CBA są dopisane do okręgu, stąd |∡CO1A| = 2α i |∡AO2B| = 2β. Z własności sumy kątów wewnętrznych w czworokącie O1O2BC wynika, że α+β = 90°, a tym samym, że trójkąt CAB jest prostokątny. Stosując wzory trygonometryczne w zaznaczonych trójkątach prostokątnych, otrzymujemy sinα = 6/10 = 4/R, skąd R = 20/3 oraz sinβ = 8/10 = 3/r, skąd r = 15/4.