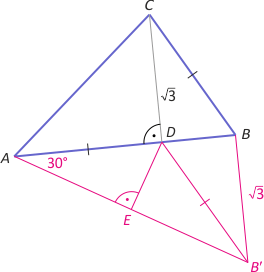
Zad. 1. W trójkącie ABC mamy |AB|=3, wysokość CD opuszczona na AB ma długość √3 oraz |AD| = |BC|. Oblicz długość AC.
Zad. 2. Dwa okręgi przecinają się w punktach A i B. Dowolna sieczna przechodząca przez B przecina pierwszy okrąg w punkcie C, a drugi w punkcie D. Styczne do okręgów w punktach C i D przecinają się w punkcie M. Przez punkt przecięcia prostych AM i CD przechodzi prosta równoległa do CM i przecina AC w punkcie K. Wykaż, że prosta KB jest styczna do drugiego okręgu.
Zad. 3. Przeciwprostokątna trójkąta ma długość 12, a jego pole wynosi 18. Znajdź miary kątów ostrych trójkąta.
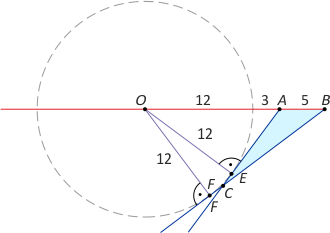
Zad. 4. (wolna amerykanka) Na prostej przechodzącej przez środek O okręgu o promieniu 12 obrano punkty A i B tak, że |OA| = 15 i |AB| = 5. Z punktów A i B poprowadzono styczne do okręgu, przy czym punkty styczności leżą po jednej stronie prostej AB. Oblicz pole trójkąta ABC, gdzie C jest punktem przecięcia stycznych
Za zadania 1-3 komplet 30 punktów otrzymali: Dominik Bysiewicz (student matematyki na UJ), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM) oraz Radosław Górzyński (uczeń, I LO Lubin).
20 pkt. uzyskał Tadeusz Porzucek (emerytowany nauczyciel z Gostynia).
Za zadanie 4 po 10 punktów otrzymali: Dominik Bysiewicz, Elżbieta Grzechnik, Mikołaj Popek, Tadeusz Porzucek oraz Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy). Gratulujemy!
Z przyjemnością informujemy, że Dominik Bysiewicz zajął I miejsce w XXI Mistrzostwach Polski w Geometrii Elementarnej rozegranych 3 VI we Wrocławiu. Udany był też występ Radosława Górzyńskiego, który zajął XVI miejsce. Gratulujemy!
Zad. 1. Niech B' będzie takim punktem, że odcinki CD i BB' są równoległe i mają równe długości. Wówczas czworokąt CDB'B jest równoległobokiem, a trójkąt AB'D jest równoramienny. Z twierdzenia Pitagorasa w trójkącie AB'B mamy |AB'| = 2√3. Zauważmy, że trójkąt AB'B jest ekierkowy i |∡BAB'|=30°. Niech DE będzie wysokością. Wówczas |AE|=√3. Z kolei trójkąt AED także jest ekierkowy i |AD|=2. Ostatecznie z twierdzenia Pitagorasa w trójkącie ADC mamy |AC|=√7.
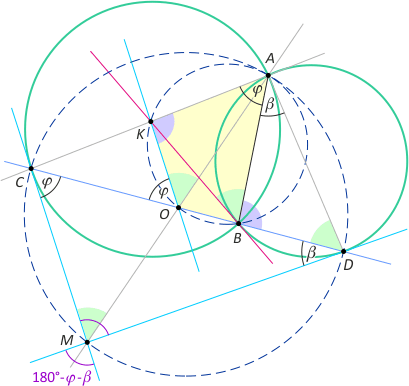
Zad. 2. Oznaczmy punkt przecięcia prostych AM i CD przez O i niech |∡BCM|=φ, a |∡BDM|=β. Kąty BCM i BDM są dopisane do okręgu, stąd kąty wpisane w ten okręg mają miary |∡CAB)=φ i |∡BAD|=β oraz |∡CAD|=φ+β. Z drugiej strony w trójkącie CMD mamy |∡CMD|=180°–(φ+β), co oznacza, że na czworokącie CMDA można opisać okrąg, a kąty CMA i CDA jako wpisane oparte na tym samym łuklu są przystające. Z równoległości prostych KO i CM wynika, że |∡COK|=φ oraz |∡KOA|=|∡CMA|. Zauważmy, że kąty zewnętrzne AKO i ACB są przystające i mają miarę φ+|∡ACB|. Oznacza to, że punkty K, O, B i A leżą na jednym okręgu. Zatem |∡KBA|=|∡KOA|=|∡BDA|, co oznacza, że prosta KB jest styczna do okręgu.
Zad. 3. Z danych wynika, że |CH|=3. Niech M będzie środkiem boku AB. Wówczas długość środkowej |CM|= |AB|/2 = 6. Zauważmy, że trójkąt CHM jest ekierkowy i |∡HMC|=30° (kąt zewnętrzny w trójkącie CMD). Stąd wynika, że w trójkącie równoramiennym CMB mamy |∡MBC|=|∡MCB|=15°, a to oznacza, że |∡CAB|=75°.
Zad. 4. Zauważmy, że trójkąty OEA i OFB są pitagorejskie o bokach 15, 12, 9 oraz 20, 12, 16. Mamy sin|∡BAC| = sin(180°–|∡OAE|) = sin|∡OAE| = 4/5, a cos|∡BAC| = -3/5. Z drugiej strony sin|∡ABC| = 3/5, a cos|∡ABC| = 4/5. Łatwo obliczyć, że sin|∡ACB| = 7/25. Z twierdzenia sinusów w trójkącie ACB mamy 5:(7/25) = |AC|:(4/5), skąd |AC| = 75/7. Ostatecznie PACB = |AB|·|AC|·sin|∡BAC|/2 = 5·(75/7)·(4/5)/2 = 150/7 = 21 i 3/7.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
