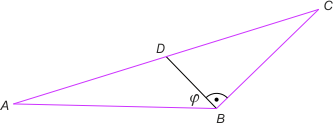
Zad. 1. W trójkącie ABC poprowadzono dwusieczne kątów A i C. Niech P i Q oznaczają rzuty prostokątne wierzchołka B na te dwusieczne. Wykaż, że odcinek PQ jest równoległy do boku AC.
Zad. 2. Wykaż, że jeśli w trójkącie jeden z kątów ma miarę 120°, to trójkąt wyznaczony przez spodki jego dwusiecznych jest prostokątny.
Zad. 3. Na boku BC w trójkącie ABC obrano punkt D taki, że |CD| = k·|AC|. Promień okręgu opisanego na tym trójkącie wynosi R. Znajdź odległość między środkami okręgów opisanych na trójkątach ABC i ADB.
Zad. 4. (wolna amerykanka) W trójkącie ABC punkt D jest środkiem boku AC, |∡DBC| = 90° oraz |BD| = √3/4|AB|. Znajdź miarę kąta ABD.
Za rozwiązania zadań 1-3 maksimum punktów zdobyli: Robert Ciężabka (student AGH), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Michel Migas (student matematyki PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Mikołaj Sikora (III LO Tarnów) oraz Paweł Wesołowski (II LO Końskie).
W kategorii "wolnej amerykanki" 10 punktów zdobyli: Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Robert Ciężabka, Wojciech Tomiczek (inżynier, Lipowa), Sabina Khady Sy (studentka nanotechnologii, UJ) oraz Szymon Kaźmierowski.
Gratulacje!
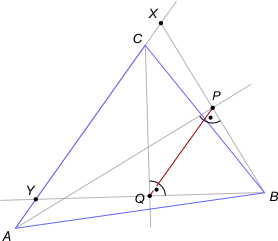
Zad. 1. Przedłużmy odcinki BP i BQ do przecięć z prostą AC w punktach X i Y. Zauważmy, że proste AP i CQ są jednocześnie symetralnymi odcinków BX i BY. Oznacza to, że P i Q są środkami tych odcinków. Zatem odcinek PQ jest linią średnią trójkąta YBX. Stąd teza.
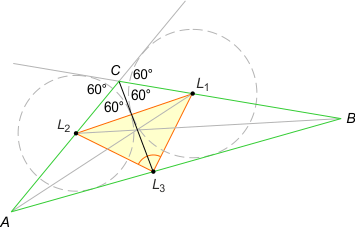
Zad. 2. Zauważmy, że L1 i L2 są środkami okręgów dopisanych do trójkątów CL3A i CL3B. Zatem odcinki L2L3 i L1L3 są prostopadłe, bo są dwusiecznymi kątów przyległych. Stąd teza.
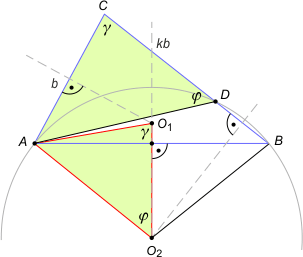
Zad. 3. Niech |∡ACB| = γ i |∡ADC| = φ. Wówczas |∡AO1O2| = γ, bo jest to połowa kąta środkowego AO1B (o mierze 2γ) w okręgu opisanym na trójkącie ABC. Z drugiej strony kąt ADB wpisany w okrąg opisany na trójkącie ADB ma miarę 180°–φ. Łatwo można obliczyć, że kąt wypukły AO2B ma miarę 2φ, a stąd |∡AO2O1| = φ, bo O1O2 jest symetralną odcinka AB. Oznacza to, że trójkąty ADC i AO1O2 są podobne (cecha kkk). Mamy zatem równość O1O2/CD = AO1/AC, skąd po podstawieniu danych otrzymujemy O1O2 = k·R.
Zad. 4. W rozwiązaniu stosujemy metodę wektorową. Ponieważ BD = (BA+BC)/2, mamy 3a2/16 = |BD|2 = BD2 = BD•BD = BD•((BA+BC)/2) = (BD•BA + BD•BC)/2 = (BD•BA + 0)/2 = (a·(a(√3)/4)·cosφ)/2. Stąd otrzymujemy cosφ = √3/2 i dalej φ = 30°.