Firma szyjąca mundurki szkolne bada wzrost sześciolatków w oparciu o dane zebrane w jednej z klas pierwszych jednej z wrocławskich szkół podstawowych. Jest sprawą oczywistą, że w klasie tej są dzieci niższe i wyższe, a różnica wzrostów między najwyższym i najniższym dzieckiem może wynosić nawet ponad 15 cm. Kierownictwo firmy postawiło pytaniem, jaki jest w typowy wzrost dziecka w tym wieku (czyli jakich mundurków potrzeba na rynku najwięcej).
Nie ma jednej dobrej odpowiedzi na tak postawione pytanie. Można jej udzielać na rozmaite sposoby. Można na przykład podać taki przedział, że wzrost tylko pewnej (niewielkiej) części dzieci z klasy nie będzie się w nim mieścił, przy czym w klasie będzie parę dzieci wyższych niż najwyższy wzrost zawarty w podanym przedziale oraz parę dzieci niższych niż najniższy wzrost mieszczący się w podanym przedziale.
Okazuje się jednak, że kierownictwo firmy oczekuje podania jednej liczby, która pozwoli opisać cały zbiór danych. Liczby, którą można by potraktować, jako przybliżenie wszystkich zebranych danych.Ale na takie pytanie także można odpowiedzieć na różne sposoby.
Zapewne wielu czytelnikom przychodzi w tym miejscu na myśl średnia arytmetyczna wszystkich zebranych wzrostów. Rzeczywiście jest ona często wykorzystywana w praktyce jako przybliżenie zbioru zebranych danych. Mamy z nią do czynienia na przykład w wypadku ocen szkolnych, kiedy średnią trzeba podać np. do wniosku stypendialnego, albo gdy rozstrzyga się, czy uczeń otrzyma promocję do następnej klasy z wyróżnieniem (czyli tzw. świadectwo z paskiem). Wówczas średnia arytmetyczna ocen na świadectwie musi wynosić co najmniej 4,75. Przypomnijmy, że średnią arytmetyczną dla zbioru liczb obliczamy, sumując zebrane dane a następnie dzieląc uzyskany wynik przez liczbę składników. Możemy ogólnie zapisać, że średnia arytmetyczna liczb x1, x2, ..., xn wynosi
[tex]\frac{1}{n}(x_1 + x_2 + \dots + x_n)[/tex].
Trzeba dodać, że średnia arytmetyczna nie jest jedyną wielkością, która "uśrednia" wartość zbioru liczb, a samo słowo "średnia" występuje w nazwach innych pojęć (np. średnia geometryczna, średnia harmoniczna i inne). Jednak my, mówiąc krótko "średnia" będziemy mieli ma myśli właśnie średnią arytmetyczną.
Oczywiście zastępowanie całego zbioru danych przez jedną liczbę, która te dane "uśrednia" ma wiele wad.
Przykład 1. Janek Kowalski z V a ma same piątki ze wszystkich przedmiotów obowiązkowych oprócz języka polskiego i historii, z których uzyskał ocenę dostateczną. Zakładając, że uczy się dziewięciu przedmiotów obowiązkowych, oblicz średnią jego ocen i ustal, czy może otrzymać świadectwo z paskiem na koniec V klasy.
Rozwiązanie. Średnia ocen Janka wynosi [tex]\frac{1}{9}(5+5+5+5+5+5+5+3+3)=\frac{41}{9}\approx 4,56[/tex]. W takiej sytuacji często można usłyszeć, że "oceny z polskiego i historii popsuły mu średnią". Nie wnikając w przyczyny, które sprawiły, że Janek dostał tróje z obu wymienionych przedmiotów, trzeba stwierdzić, że z właśnie z ich powodu nie dostał świadectwa z paskiem, chociaż trudno go uznać za słabego ucznia, skoro poza dwiema trójkami ma same piątki z siedmiu przedmiotów.
Powyższy przykład pokazuje główną słabość średniej jako przybliżenia zbioru danych: średnia jest nieodporna na na tzw. obserwacje odstające (tzn. takie, które są zdecydowanie większe lub zdecydowanie mniejsze od pozostałych obserwacji), nawet jeśli odstających obserwacji jest niewiele.
Zbiór obserwacji można też przybliżyć za pomocą jednej liczby w inny sposób. Postępujemy następująco: ustawiamy wszystkie dane w porządku rosnącym (lub malejącym) i wybieramy spośród nich tę, która znajduje się w środku, gdy liczba obserwacji jest nieparzysta, albo bierzemy średnią arytmetyczną dwóch środkowych liczb, gdy liczba wszystkich jest parzysta. Uzyskaną w ten sposób wartość nazywamy medianą.
Mediana dla ocen Janka Kowalskiego wynosi 5, a więc tyle samo, co dla ucznia, który miałby na świadectwie same piątki. Uczniowie Ci mieliby zupełnie inne średnie ocen, ale pod względem mediany ocen byliby zrównani w osiągnięciach.
Przykład 2. Oblicz średnią i medianę dla zestawu liczb 2, 2, 6, 2, 6, 2, 6, 3, 7, 7 oraz dla tego samego zestawu z dołożoną liczbą 1.
Rozwiązanie. Po ustawieniu liczb w kolejności rosnącej, otrzymujemy ciąg: 2, 2, 2, 2, 3, 6, 6, 6, 7, 7. Wszystkich liczb jest 10, wobec tego medianą jest średnia piątej i szóstej liczby tj. liczb 3 i 6. Wynosi ona (3+6):2 = 4,5. Natomiast średnia tych liczb to (4·2+3+3·6+2·7):10 = 43:10 = 4,3. Gdyby do zestawu danych dołożyć jeszcze liczbę 1, to wszystkich liczb byłoby 11, więc mediana byłaby szóstą liczbą w kolejności, czyli byłaby równa 3, a średnia wynosiłaby 44:11 = 4.
Średnią i medianę określamy wspólną nazwą miar położenia danych. Dają one wyobrażenie o tym, gdzie zebrane dane leżą na osi liczbowej, tzn. czy są to liczby duże, czy też małe.
[koniec wykładu dla gimnazjalistów]
Zajmowaliśmy się do tej pory problemem znalezienia jednej liczby, za pomocą której można by w miarę dokładnie przybliżyć cały zestaw danych liczb. A jak można to zrobić najdokładniej? Jak porównywać dokładność takich przybliżeń? Dla liczb x1, x2, ... , xn poszukajmy takiej liczby a, której odległość od zestawu tych liczb będzie najmniejsza. Tylko jak mierzyć odległość między jedną liczbą a zestawem danych? Znowu można to zrobić na kilka sposobów.
Gdybyśmy mieli do czynienia z jednoelementowym zestawem danych złożonym tylko z liczby x, to odległość liczby a od tego zestawy zmierzylibyśmy jako odległość liczb a i x, czyli jako |x-a| = [tex]\sqrt{(x-a)^2}[/tex]. Uogólniając ten sposób mierzenia odległości a do wielu innych liczb, możemy jako jedną z metod wskazać sumowanie odległości między liczbą a i kolejnymi liczbami z zestawu x1, x2, ..., xn. W ten sposób otrzymamy |x1-a|+|x2-a|+...+|xn-a|. Można też postąpić inaczej: dodać kwadraty odległości a od poszczególnych liczb z zestawu, a następnie wyciągnąć pierwiastek z takiej sumy. Otrzymamy wówczas:
[tex]\sqrt{(x_1-a)^2+(x_2-a)^2+\dots+(x_n-a)^2}[/tex].
Można udowodnić, że pierwsze wyrażenie osiąga najmniejszą wartość, jeśli za a wstawimy medianę liczb x1, x2, ..., xn, natomiast drugie - jeśli za a wstawimy ich średnią. Zatem w zależności od tego, w jaki sposób zdefiniujemy odległość liczby od zestawu danych i w jaki sposób określimy przybliżenie zbioru liczb za pomocą jednej liczby, będziemy uzyskiwali potencjalnie różne wyniki. Co więc wybrać jako uśrednienie i reprezentację całego zbioru liczb: średnią czy medianę, a może jeszcze jakąś inną wielkość? O tym opowiemy w następnych odcinkach Ligi.
Zadanie 1. Oblicz średnią i medianę zestawu liczb: 3,1; -4,8; 0,6; 4,1; -4,8; 3,7; 2,7; -3,3; -4,6; -2,7; 3,2; 4,1.
Zadanie 2. Wiadomo, że średnia pewnych liczb wynosi 13,8. Jeśli do zestawu dodamy jeszcze jedną liczbę, to suma liczb zwiększy się o 41, a średnia będzie wynosiła 17,2. Ile było wyjściowych liczb?
Zadanie 3. Dzieci w pewnej klasie zapytano, ile mają rodzeństwa. Troje z nich było jedynakami, dziesięcioro miało tylko brata lub siostrę, ośmioro miało dwoje rodzeństwa, troje pochodziło z rodziny czworodzietnej i jedno z pięciodzietnej. Ile wynosiła średnia i mediana liczby rodzeństwa u dzieci w tej klasie?
Zadanie 1. Pokaż, że w przypadku drugiego sposobu mierzenia odległości liczby a od zestawu liczb 1, 5, 7, 10, 14, odległość ta będzie najmniejsza dla a równego średniej liczb z tego zestawu.
Zadanie 2. Dla zestawu liczb z zadania 1 pokaż, że w przypadku pierwszego sposobu mierzenia odległości liczby a od zestawu liczb, odległość ta będzie najmniejsza dla a równego medianie liczb z tego zestawu.
Zadanie 3. Wykonaj zadanie 1 dla dowolnego zestawu danych x1, x2, ..., xn.
Wskazówka. Pamiętaj, że pierwiastek kwadratowy jest funkcją rosnącą, zatem im mniejsza jest wartość pierwiastkowanej liczby (o ile jest dodatnia), tym mniejsza jest wartość pierwiastka z niej. Czyli pierwiastek kwadratowy osiąga najmniejszą wartość wtedy, gdy wyciągany jest z najmniejszej liczby. Zatem symbol pierwiastka w minimalizowanym wyrażeniu można pominąć.
Za rozwiazania pierwszej serii ligowych zadań maksymalną możliwą liczbę 3 punktów uzyskali:
- Aleksandra Domagała
z G 23 we Wrocławiu, - Kaja Grabowska
z G 2 w Wołowie, - Joanna Lisiowska z Katolickiego G w Warszawie,
- Daniel Sokulski z G 2 w Olsztynie,
- Kacper Toczek z G 2 w Wołowie.
Mieszko Baszczak z SP 301 w Warszawie otrzymał 2,5 pkt. Pozostali Zawodnicy uzyskali poniżej 2 pkt.
Wśród uczniów szkół ponadgimnazjalnych nikt w tym miesiącu nie uzyskał maksymalnej liczby punktów. Do czołówki należą:
- Tomasz Stempniak z I LO w Ostrowie Wielkopolskim (2,5 pkt),
- Daria Bumażnik z II LO w Jeleniej Górze (2 pkt),
- Krzysztof Danielak z I LO w Jeleniej Górze (2 pkt).
Wszystkim gratulujemy i zachęcamy do rozwiazywania zadań statystycznych w kolejnych miesiącach.
Zad. 1. Średnia podanych liczb wynosi 13/120 = 0,108(3) ≈ 0, 0,11. Mediana jest
równa średniej arytmetycznej szóstej i siódmej z podanych dwunastu liczb, a zatem wynosi 0,6+2,7/2 = 1,65.
Zad. 2. Niech n oznacza liczbę obserwacji, których średnią obliczamy, a S - ich sumę. Należy rozwiązać układ równań: S/n = 13,8 i S+41/n+1 =17,2. Otrzymamy n=7.
Zad. 3. W klasie było 25 uczniów. Średnia liczba rodzeństwa wynosiła 1/25 (3·0+10·1+8·2+3·3+1·4) = 1,56. Mediana jest trzynastą liczbą w kolejności, czyli jest równa 1.
Zad. 1. Poszukujemy wartości a, która minimalizuje wyrażenie [tex]\sqrt{(1-a)^2+(5-a)^2+(7-a)^2+(10-a)^2+(14-a)^2}[/tex].
Zgodnie ze wskazówką wystarczy zminimalizować wyrażenie podpierwiastkowe
(1-a)2+(5-a)2+(7-a)2+(10-a)2+(14-a)2, które po uporządkowaniu jest równe 371-74a+5a2. Osiąga ono minimum dla a = - -74/2·5 = 7,4. Jednocześnie 7,4 jest średnią liczb 1, 5, 7, 10 i 14.
Zad. 2. Poszukujemy wartości a, która minimalizuje wyrażenie
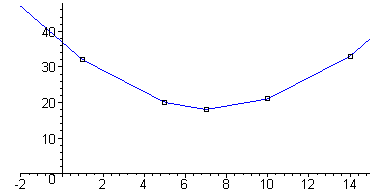
|1-a|+|5-a|+|7-a|+|10-a|+|14-a|. Wyrażenie to definiuje pewną funkcję zmiennej a, która jest ciągła. Jej wykres jest łamaną złożoną z czterech odcinków i dwóch półprostych będących fragmentami wykresów funkcji liniowych określonych na przedziałach: (-∞, 1), [1, 5), [5, 7), [7, 10), [10, 14), [14, ∞). Możemy wyznaczyć wzór tej funkcji i sporządzić jej wykres (patrz rysunek), jednak wystarczy zauważyć, że w pierwszych trzech przedziałach wykres składa się z fragmentów wykresów funkcji malejących, a w trzech kolejnych - z wykresów funkcji rosnących. Wobec tego rozważana funkcja jest malejąca w przedziale (-∞, 7) i rosnąca w przedziale [7, ∞), zatem osiąga minimum dla a=7. Jednocześnie 7 jest medianą liczb 1, 5, 7, 10 i 14.
Zad. 3. Postępujemy podobnie jak w zadaniu 1, opuszczając pierwiastek w minimalizowanym wyrażeniu. Ponieważ (x1-a)2+(x2-a)2+...+(xn-a)2 = (x12+x22+...+xn2)-2a(x1+x2+...+xn)+na2, wyrażenie to osiąga minimum dla a =-[tex]\frac{-2(x_1+x_2\dots+x_n)}{2n}[/tex]= 1/n(x1+x2+...xn).







