Zad. 1. Wierzchołki 33-kąta foremnego pokolorowano na czerwono lub niebiesko, przy czym wiadomo, że
- jeśli dwa wierzchołki sąsiadują, to maksymalnie jeden spośród nich jest czerwony;
- jeśli pomiędzy dwoma wierzchołkami znajduje się dokładnie 15 innych, to także maksymalnie jeden spośród tych dwóch jest czerwony.
Ile maksymalnie wierzchołków pokolorowano na czerwono?
Zad. 2. Na tablicy napisano liczbę n4+½n2−1 dla każdej naturalnej dwucyfrowej n. W przypadku ilu liczb zapisanych na tablicy ostatnią cyfrą w ich zapisie dziesiętnym jest 5?
Zad. 3. Ile jest liczb pięciocyfrowych, w których zapisie dziesiętnym każde dwie sąsiednie cyfry są różne?
W tym miesiącu punkty zdobyli:
- 11 – Igor Sudyka (SP 2 Jasło)
- 8 – Aleksander Porębny (SP 113 Wrocław).
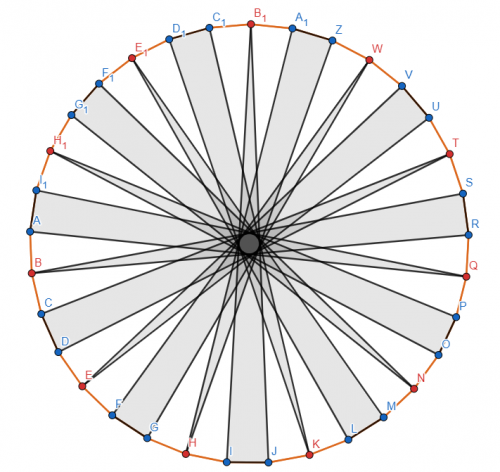
Zad. 1. Wierzchołki 33-kąta mozemy podzielić na 11 rozłącznych grup, jak na rysunku. W każdej z nich co najwyżej jeden wierzchołek może być czerwony. Wobec tego czerwonych wierzchołków może być maksymalnie 11. Przykładowe kolorowanie wierzchołków zamieszczono na rysunku.
Zad. 2. Rozważymy n parzyste. Wówczas liczba n4+½n2−1 jest całkowita. Pomnóżmy to wyrażenie przez 2. Otrzymamy 2n4+n2−2. Modulo pięć 2n4 przystaje do 0 lub 2; n2 do -1, 0 lub 1, a -2 przystaje oczywiście do -2. Suma nie może zatem przystawać do zera modulo 5. Dlaczego wykluczamy układ reszt 2;0;-2? Skoro dwukrotność pierwotnego wyrażenia nie jest podzielna przez 5, także to wyrażenie nie może być podzielne przez 5, a ponieważ wartość jest całkowita i niepodzielna przez 5, nie kończy się piątką.
Jesli natomiast n jest nieparzyste, to n4−1 jest całkowite, a ½n2 ma część ułamkową równą ½, czyli w zapisie dziesiętnym kończy się na 5. Podsumowując, warunki zadania są spełnione tylko przez liczby nieparzyste. Na tablicy zapisano 45 liczb naturalnych dwucyfrowych.
Zad. 3. Na pierwszym od lewej miejscu w zapisie dziesiętnym liczby pięciocyfrowej możemy umieścić jedną z dziewięciu cyfr (od 1 do 9). Na każde kolejne miejsce mamy do wyboru jedną z dziewięciu cyfr (od 0 do 9 z wyjątkiem cyfry wybranej poprzednio). Mamy zatem pięć niezależnych wyborów dziewięciu opcji. Odpowiedzią jest 95.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
