Zad. 1. W trójkącie równobocznym ABC na bokach BC i CA obrano punkty D i E. Odcinki AD i BE przecinają się w punkcie K. Wiedząc, że PEKDC = PAKB, oblicz miarę kąta DKB.
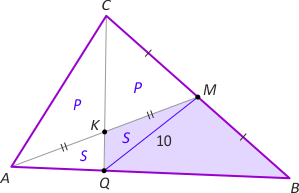
Zad. 2. W trójkącie ABC punkt M jest środkiem boku BC, a punkt K - środkiem odcinka AM. Prosta CK przecina bok AB w punkcie P. Wiedząc, że pole czworokąta PBMK wynosi 10, oblicz pole trójkąta ABC.
Zad. 3. W trójkącie ABC środkowa AD i dwusieczna CE są wzajemnie prostopadłe i przecinają się w punkcie F, który jest środkiem odcinka AD. Wiedząc, że PFED=5, oblicz pole trójkąta ABC.
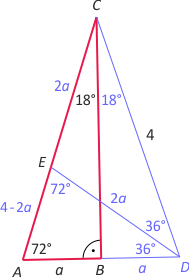
Zad. 4. (wolna amerykanka) Oblicz długości boków prostokąta, w którym przekątna o długości 4 tworzy z bokiem kąt o mierze 72°. Odpowiedź podaj w postaci a√b + c.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Norbert Kaczmarek (pracownik budowlany, Secemin), Milena Kwiatkowska (uczennica XIV LO Warszawa), Sławomir Matysiak (nauczyciel X LO Wrocław), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Mikołaj Popek (student UAM), Michał Smółko (uczeń XIV LO Warszawa),
- 28 - Mateusz Kula (doktorant matematyki na UŚ), Marzena Wąsiewicz (nauczycielka z Kajetan),
- 26 - Mikołaj Michalik (uczeń XIV LO Warszawa).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Norbert Kaczmarek, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mateusz Kula, Tadeusz Porzucek, Mikołaj Popek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Z założenia wynika równość pól trójkątów ADC i ABE oraz równość ich wysokości DM i EN (są opuszczone na równe podstawy). To oznacza przystawanie trójkątów CMD i ANE (z cechy bkb), skąd otrzymujemy |AE|=|CD| i przystawanie trójkątów ABE i ADC (z cechy bkb). Przy przyjętych oznaczeniach łatwo zauważyć, że szukany kąt jest zewnętrznym w trójkącie AKB i ma miarę 60°.
Zad. 2. Niech P i S oznaczają pola odpowiednich trójkątów. CK i QK są środkowymi trójkątów AMC i APM, a QM i AM są środkowymi trójkątów ABM i ABC. Otrzymujemy równania P+S = 10–S oraz 2P = 10+S, skąd S=2 i P=6. Ostatecznie szukane pole trójkąta ABC wynosi 24.
Zad. 3. Z założenia wynika, że trójkąt ADC jest równoramienny oraz |BC| = 2|AC|. Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy |EB| = 2|AE|, co oznacza, że pole trójkąta EBD jest dwa razy większe od pola trójkąta AED, które wynosi 10, bo EF jest jego środkową. Ostatecznie szukane pole trójkąta wynosi 60.
Zad. 4. (wolna amerykanka) Dorysujmy trójkąt BDC symetryczny do wyjściowego. Otrzymujemy trójkąt równoramienny ADC. Niech DE będzie dwusieczną kąta D. Zauważmy, że powstały dwa trójkąty równoramienne ADE oraz DEC, przy czym |AD|=|DE|=|EC|=2a oraz |AE|=4–2a. Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy równanie 2a/4 = (4–2a)/2a, skąd otrzymujemy a = √5–1 i dalej |BC| = √(10+2√5).
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
