Zad. 1. Liczbą palindromiczną nazywamy taką liczbę naturalną, która nie zmienia wartości czytana w przód i wspak. Ile jest liczb palindromicznych pięciocyfrowych?
Zad. 2. Pani Anna wybiera się na grzybobranie. Uzbierane borowiki wysuszy i przygotuje z nich zupę krem. Świeże grzyby zawierają 90% wody, a po wysuszeniu - tylko 15% wody. Ile co najmniej borowików musi nazbierać pani Anna, aby przygotować zupę z 5 dag suszonych grzybów?
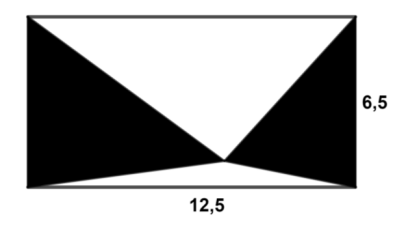
Zad. 3. Oblicz pole powierzchni zacieniowanej części figury z poniższego rysunku.
W październiku punkty zdobyli:
- 3 – Szczepan Buczkowski SP 2 Ożarów Mazowiecki, Wiktor Gatner SP 24 Wrocław, Zuzanna Garbecka SP 2 zczytno, Aleks Górniak SP Regent College Elbląg, Michał Górniak SP Regent College Elbląg, Paweł Jarzyński SP 13 Zielona Góra, Adam Kosarzycki SP 16 Wrocław, Joanna Kubik SP 3 Oleśnica, Emilia Piasta SP Płomień Katowice, Mateusz Plaminiak SP 39 Wrocław, Natasza Sosnal SP 16 Wrocław, Yaraslau Sialiuk SP 82 Wrocław, Filip Staszkiewicz SP 50 Wrocław, Marcin Węgrzyn SP 44 Wrocław, Ignacy Włodarski SP 36 Wrocław, Michał Wróblewski SP Bielkówko, Dawid Zysk SP 19 Legnica;
- 2 – Filip Augustyniak SP 50 Wrocław, Zuzanna Bylińska SP 19 Legnica, Jakub Derewecki SP 50 Wrocław, Adam Gajdzis SP 107 Wrocław, Claudia Jończyk SP Jedlnia Letnisko, Darya Karnitskaya SP 107 Wrocław, Pola Kuczwara SP 29 Wrocław, Hanna Kulpińska SP 50 Wrocław, Hanna Łukasik SP 50 Wrocław, Igor Pac SP 2 Szczytno, Alicja Picińska 64 Wrocław, Wiktor Szwarczyński SP Szkoła w chmurze Poznań, Adam Teleśnicki SP 50 Wrocław, Kacper Ziółek SP 2 Szczytno;
- 1 – Natalia Bulak SP 3 Ścinawa, Karolina Grzyb SP Płomień Katowice, Emilia Łakomiec SP 50 Wrocław, Stanisław Solski SP 13 Zielona Góra, Lena Szkirpan SP 50 Wrocław, Emilia Wahl SP Popielów, Ignacy Włodarski SP 36 Wrocław, Marlena Zatoń SP Płomień Katowice.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Aby liczba była palindromiczna, pierwsza i ostatnia cyfra muszą być takie same, podobnie jak druga i przedostatnia. Środkowa cyfra może być dowolna. Liczba pięciocyfrowa nie może zaczynać się od zera, dlatego dla pierwszej cyfry mamy 9 możliwych wyborów (od 1 do 9) i jeden wybór dla cyfry piątej. Mamy 10 możliwości wyboru dla cyfry drugiej (od 0 do 9) i jeden dla czwartej oraz 10 możliwości wyboru dla cyfry trzeciej (od 0 do 9). Wyborów tych dokonujemy niezależnie, zatem z reguły iloczynu liczb palindromicznych pięciocyfrowych jest 9.10.10 = 900.
Zad. 2. Wysuszone grzyby zawierają 15% wody, co oznacza, że pozostałe 85% ich masy stanowi grzyb (bez wody). W 5 dag suszonych grzybów znajduje się więc 0,85.5 = 4,25 dag grzyba. Ponieważ masa suchej części nie zmienia się podczas suszenia, w nazbieranych świeżych grzybach musi być co najmniej 4,25 dag grzyba. Świeże grzyby zawierają 90% wody, co oznacza, że 10% ich masy stanowi grzyb, zatem aby uzyskać 4,25 dag suchej masy grzyba, świeżych grzybów trzeba zebrać co najmniej 4,25.10 = 42,5 dag.
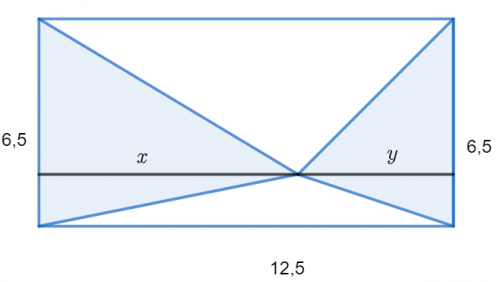
Zad. 3. Oznaczmy przez x i y wysokości zacieniowanych trójkątów. Suma ich długości wynosi x+y = 12,5. Pole zacieniowanej figury wynosi: 0,5.6,5.x + 0,5.6,5y = 3,25.x+3,25y = 3,25(x+y) = 3,25.12,5 = 40,625.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
