Zad. 1. Ile wynosi x+y+z, jeśli wiadomo że trójka (x, y, z) jest rozwiązaniem układu równań: [TEX]\left\{\begin{array}{rcl}xy&=&-3\\yz&=&-6\\zx&=&2\end{array}\right.[/TEX]
Zad. 2. Czy liczba 411+524+1012 jest pierwsza? Odpowiedź uzasadnij.
Zad. 3. W okrąg o promieniu R wpisano trójkąt prostokątny tak, aby promień okręgu wpisanego w ten trójkąt był jak największy. Ile wynosi promień okręgu wpisanego? Odpowiedź uzasadnij.
W tym miesiącu punkty zdobyli:
- 3 - Jakub Dobrzański G 3 Lubin, Kacper Gembara G w ZSS Wołów, Kinga Kędzierska G Solec, Marek Komorowski G 3 Żory, Wiktor Koropczuk G 3 Gorzów Wielkopolski, Oliwia Kropidłowska G 1 Wrocław, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Michał Romański G Eureka Poznań, Przemysław Rybarczyk G Integracyjne Stargard i Laura Stefanowska G im. św. Franciszka z Asyżu Legnica;
- 2,5 - Emilia Kapłon G Żary, Julia Mazur G Lewin Brzeski, Karolina Mielczarek G Lewin Brzeski, Katarzyna Siomka G Lewin Brzeski i Kajetan Walawski G Leżajsk;
- 2 - Helena John G Wielowieś Świniowice, Krzysztof Mach G 52 Kraków i Franciszek Stepek G Społeczne Żary;
- 1 - Michał Fabijanowski Niepubliczne G Nasza Szkoła Warszawa, Przemysław Lewandowski G Sochocin i Maciej Lisak G 1 Krosno.
Pozostali uczestnicy otrzymali poniżej 0,5 punktu.
Po czterech miesiącach Ligi Zadaniowej z wynikiem 12 pkt. (na 12 możliwych) prowadzą: Jakub Dobrzański, Wiktor Koropczuk, Oliwia Kropidłowska, Joanna Lisiowska, Konrad Litwiński i Przemysław Rybarczyk, drugie miejsce z wynikiem 11,5 pkt. zajmuje Marek Komorowski, a trzecie miejsce z wynikiem 11 pkt. zajmują: Kacper Gembara i Laura Stefanowska. Gratulujemy!
Zad. 1. Podany układ równań ma dwa pierwiastki: (1, -3, 2) oraz (-1, 3, -2). W obu przypadkach x+y+z wynosi 0.
Zad. 2. Liczba 411+524+1012 jest złożona, bo równa się 211·2 + 212·512 + 512·2 = (211+512)2.
Zad. 3. Największy promień okręgu wpisanego w trójkąt prostokątny wpisany w dany okrąg uzyskamy wtedy, gdy trójkąt ten będzie równoramienny (wyjaśnienie poniżej). Długość promienia okręgu wpisanego w dowolny trójkąt wynosi r = 2·pole/obwód (dlaczego?). Pole i obwód trójkąta prostokątnego równoramiennego wpisanego w okrąg o promieniu R wynoszą odpowiednio R2 i 2R(1+√2) - dlaczego? Stąd r = R(√2–1).
Lemat. Ze wszystkich trójkątów prostokątnych wpisanych w dany okrąg największy promień okręgu wpisanego ma trójkąt równoramienny.
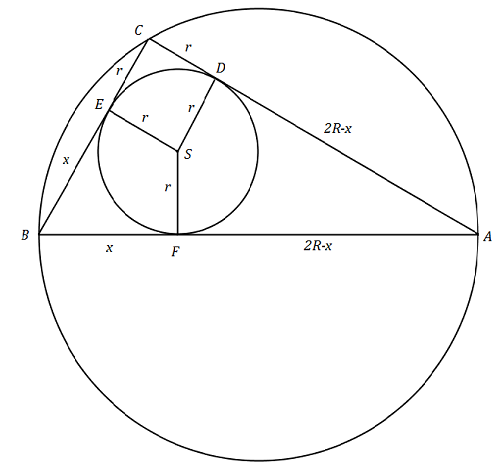
Dowód. Pole trójkąta ABC jest równe sumie pól kwadratu CDSE oraz deltoidów BESF i ADSF, czyli
PΔABC = r2 + xr + r(2R–x) = r2+2Rr = r(r+2R).
Ponieważ R jest ustalone, to promień r okręgu wpisanego w trójkąt ABC będzie największy, kiedy pole tego trójkąta będzie największe. Pole trójkąta prostokątnego wpisanego w okrąg jest największe, gdy ma on największą wysokość opuszczona na przeciwprostokątną (która jest jednocześnie średnicą tego okręgu). Z symetrii okręgu największą wysokość uzyskamy, gdy wierzchołek kąta prostego wypadnie w połowie półokręgu wyciętego przez tę średnicę.