W poprzednim rozdziale zostały przedstawione konstrukcje niewypukłych wielościanów jednorodnych W72 i W74, których wierzchołki znajdują się w wierzchołkach archimedesowego dwudziesto-dwunastościanu rombowego małego. W tym miejscu opiszemy wielościan jednorodny o wierzchołkach pokrywających się z wierzchołkami innego wielościanu archimedesowego - dwudziesto-dwunastościanu (rys.1). Będzie to dwudziesto-dwunastościan wielki. W książce Magnusa Wenningera 'Polyhedron Models' figuruje on pod numerem W94.
Spójrzmy na dwudziesto-dwunastościan (rys. 1). Jego ścianami są trójkąty równoboczne i pięciokąty foremne.
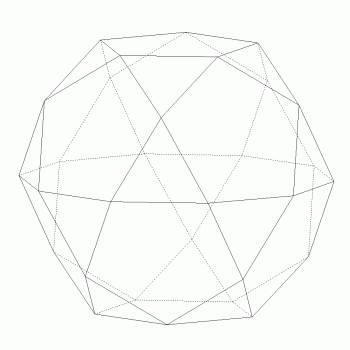
rys. 1
Zauważmy, że wybierając odpowiednio trzy wierzchołki tej bryły, możemy utworzyć pod każdą trójkątną ścianą duży trójkąt równoboczny (rys. 2).
rys. 2
Podobnie pod każdą ścianą pięciokątną możemy utworzyć pentagram (rys. 3).
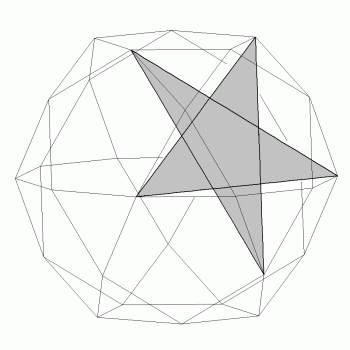
rys. 3
Można łatwo sprawdzić, że długości boków otrzymanego w ten sposób trójkąta i pentagramu są równe. Wyjściowy wielościan ma 12 ścian pięciokątnych i 20 trójkątnych, wobec tego możemy utworzyć 12 pentagramów i 20 trójkątów. Rysunek 4 przedstawia wszystkie 12 pentagramów powstałych w opisany wyżej sposób.
Na rysunkach 5–8 do tej konstrukcji są dołączane kolejne trójkąty.
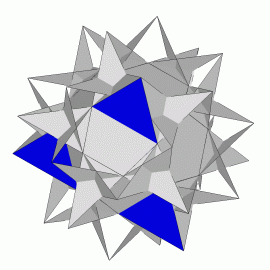
rys. 7 rys. 8
Po dołączeniu wszystkich 20 trójkątów powstaje piękny niewypukły wielościan zwany dwudziesto-dwunastościanem wielkim lub W 94 (rys. 9).
rys. 9
Sądząc z jego wyglądu, wykonanie modelu tej bryły nie powinno być specjalnie trudne. I tak jest w istocie. Przyjrzyjmy mu się nieco uważniej. Widoczne na zewnątrz fragmenty ścian będących pentagramami są deltoidami (w każdym wierzchołku) i pięciokątami foremnymi (w środku ściany). A widoczne na zewnątrz fragmenty ścian trójkątnych to nieforemne pięciokąty (po 3 na każdej ścianie). Można podejrzewać, że niektóre odcinki, wzdłuż których ściany się przecinają, są równoległe do siebie nawzajem oraz do krawędzi wielościanu. To, czego nie widać na rysunku 9, jest doskonale widoczne na rysunkach 4 – 8. Ukazują one wewnętrzną strukturę całego modelu. Na rysunku 4 można zobaczyć, że linia wzdłuż której przecinają się dwa pentagramy, przechodzi przez punkty przecięcia dwóch ramion każdego z nich. Ponadto linia przecięcia jet równoległa do jednej z krawędzi pentagramu. Kolejne rysunki pokazują, jak ściany trójkątne przecinają pojedynczy pentagram i jak przecinają się nawzajem. Pozwala to sporządzić rysunki 10 i 11, na których poprowadzone są wszystkie linie, wzdłuż których daną ścianę przecinają inne. Widoczne na zewnątrz fragmenty ścian zostały zacieniowane.
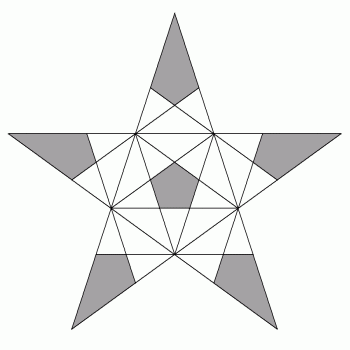
rys. 10
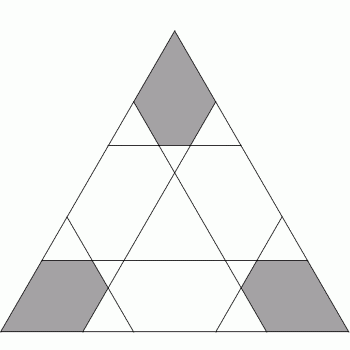
rys. 11
Spójrzmy ponownie na rysunek 9. Podpowiada on, aby model wykonać z 12 „pięciopłatkowych kwiatków” połączonych z 20 „trójliściami”. Elementy siatki przedstawia rysunek 12.
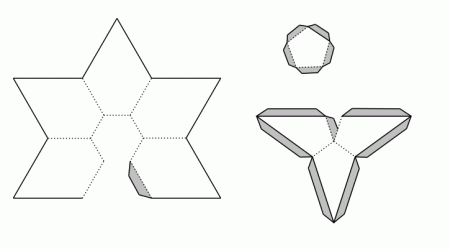
rys. 12
Ustalenie, które elementy tworzą „kwiatki”, a które „trójliście” jest nietrudne. Linie przerywane oznaczają krawędzie wklęsłe. Wykonanie modelu rozpoczynamy od przygotowania „kwiatka”. Następnie doklejamy do niego 5 „trójliści”. Potem doklejamy kolejne „kwiatki” i „trójliście” aż do ukończenia całego modelu. Poniżej zamieszczamy szablony zawierające elementy siatki pogrupowane wg rodzaju ścian. Kliknięcie w napis otwiera w nowym oknie odpowiedni rysunek. Do wykonania całego modelu potrzeba po dwie kopie każdego szablonu. Jeżeli krawędź małego pięciokąta foremnego będzie miała 1 cm, to powstanie model o średnicy około 14 cm.
Tym, którzy nie boją się wyzwań, proponujemy wykonanie modelu w 6 kolorach (5 kolorów dla ścian trójkątnych i 1 kolor dla pentagramów) – tak jak przestawia to rysunek 9. Jest to oczywiście znacznie bardziej pracochłonne, a zachowanie właściwego układu kolorów wymaga sporej uwagi (pomocny będzie rys. 9), ale efekt końcowy wart jest poczynionych starań.
Rysunki i diagramy zostały przygotowane przy użyciu programu Wingeom.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
