październik 2016

W pierwszym odcinku Ligi zadaniowej z gier logiczno-strategicznych proponuję zapoznanie się z grą dobutsu shogi, czyli uproszczoną wersją shogi (szachów japońskich). W kolejnych odcinkach pojawi się pełna wersja shogi oraz inne gry strategiczne. Wprowadzenie do zasad dobutsu shogi znajduje się tutaj.

We wszystkich zadaniach zwierzęta niewidoczne na diagramie pomijamy.

Zad. 1. Szachem nazywamy sytuację, w której Lew jest atakowany przez zwierzę przeciwnika. Na diagramie nasz Lew na A3 jest szachowany przez Żyrafę na A2. Jeśli nic z tym nie zrobimy, to w kolejnym ruchu nasz Lew zostanie zbity i przegramy. Jest tylko jeden ruch, który pozwala uniknąć natychmiastowej porażki. Jaki?

Zad. 2. Matem (lub szach-matem) nazywamy sytuację, w której Lew jest szachowany i nie istnieje sposób, żeby tego szacha uniknąć. To znaczy, że Lew zostanie zbity, niezależnie od ruchu, jaki wykonamy. Na diagramie Lew z Drużyny Nieba został na planszy sam. Jakim ruchem Drużyna Lasu może doprowadzić do mata? Takie zadanie nazywamy matem w jednym ruchu. Pamiętaj o możliwości wstawiania figur na planszę. W przedstawionej sytuacji masz do dyspozycji Słonia i Żyrafę.

Zad. 3. Jakim ruchem Drużyna Lasu może doprowadzić do wygranej w jednym ruchu? Tym razem ławka rezerwowych jest pusta, tzn. nie mamy możliwości wstawiania zwierząt. Pozornie nie mamy sensownej możliwości zaatakowania Lwa na A1, ale przypomnij sobie, kiedy możemy zdobyć dodatkowe ruchy dla zwierząt.

Zadanie dodatkowe. Standardowa szachownica ma rozmiar 8 x 8 pól, a figura szachowa zwana królem może poruszać się (i bić) o jedno pole w każdym kierunku (poziomo, pionowo i na skosy). Na jednym polu szachownicy może stać maksymalnie jedna figura.
A) Na ile sposobów można ustawić na szachownicy jednocześnie czarnego i białego króla?
B) Wśród pozycji, które zliczamy powyżej są również takie, które są nielegalne z punktu widzenia zasad gry w szachy, czyli takich, w których jeden król może zbić drugiego. Ile jest legalnych sposobów ustawienia dwóch króli?
Uzasadnij obie odpowiedzi.

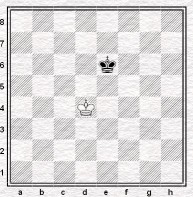Pozycja nielegalna - królowie są obok siebie.	Pozycja legalna - królowie są oddaleni o więcej niż jedno pole.

Odpowiedzi:

Zad. 1.  Zbijamy Żyrafę, przesuwając Super Kurczaka z A1 na A2. Po każdym innym ruchu nasz Lew zostanie zbity.

Zad. 2. Wstawiamy Żyrafę na C2. 

Zad. 3. Wchodzimy Kurczakiem z B2 na B1 i promujemy go na Super Kurczaka. Lew drużyny przeciwnej zostaje zamatowany.

Zadanie dodatkowe
A) Na 64 sposoby wybieramy pole dla czarnego króla i zostają 63 pola dla króla białego. 64·63 = 4032
B) Liczbę nielegalnych ustawień obliczamy poprzez analizę możliwych ustawień czarnego króla. Są trzy takie sytuacje:
   1. Czarny król jest w rogu (4 możliwe pola). Atakuje on wtedy 3 pola.
   2. Czarny król jest na bandzie, ale nie w rogu (24 możliwe pola). Atakuje on wtedy 5 pól.
   3. Czarny król jest na polu niebandowym (36 możliwych pól). Atakuje on wtedy 8 pól.
Zliczając wszystkie przypadki, otrzymujemy 4·3+24·5+36·8 = 420 nielegalnych ustawień. Zatem ustawień legalnych jest 4032–420 = 3612.

Wyniki:

W tym miesiącu punkty zdobyli:

• 3 - Konrad Andruchów - uczeń SP 4 Bolesławiec, Jadwiga Bąk - nauczycielka matematyki z Karłowic, Mikołaj Bilski - uczeń SP 6 Jelenia Góra, Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr,  Antoni Buraczewski - uczeń SP 107 Wrocław, Dominik Bysiewicz - uczeń GM Dwujęzyczne Krosno, Krzysztof Danielak - student informatyki przemysłowej na PWr, Agata Dziwok - uczennica I LO Katowice, Maja Dziwok - uczennica I LO Katowice, Kosma Kasprzak - uczeń GM 58 Poznań, Michał Korman - uczeń V LO Kraków, Marcin Kucharski - student PWr, Krystyna Lisiowska - redaktor z Warszawy, Sławomir Matysiak - nauczyciel matematyki z Trzebnicy, Szymon Meyer - student matematyki na PWr, Dawid Paradowski - uczeń VIII LO Wrocław, Andrzej Piasecki - administrator IT z Oleśnicy, Jakub Ptak - uczeń SP 64 Wrocław, Paweł Sawicki - uczeń III LO Gdynia, Krzysztof Sieja - konsultant podatkowy z Wrocławia, Karol Stanclik - uczeń LA PWr, Wojciech Tomiczek - inżynier z Lipowej, Marzena Wąsiewicz - gospodyni domowa z Kajetan, Mateusz Winiarski - uczeń GM Krosno, Marcin Wolak - uczeń I LO Kraków, Zuzanna Wołczańska - uczennica I LO Kłodzko, Piotr Wróbel - inżynier sprzedaży z Brwinowa,
• 2 - Michał Kępiński - uczeń Społ. LO Żary, Dawid Konieczko - uczeń Społ. GM Szprotawa, Dawid Migacz - uczeń I LO Tarnów, Adam Wrzesiński - terapeuta z Cieszyna,  Dominik Zygmunt - student bankowości UŁ,
• 1 - Nataniel Kędzierski - uczeń GA PWr, Michał Piórkowski - uczeń GM s. Urszulanek Wrocław

Za zadanie dodatkowe w październiku można było uzyskać 5 punktów. Punkty zdobyli:

• 5 - Mikołaj Bilski, Antoni Buraczewski, Dominik Bysiewicz, Krzysztof Danielak, Kosma Kasprzak, Dawid Konieczko, Michał Korman, Marcin Kucharski, Krystyna Lisiowska, Sławomir Matysiak, Szymon Meyer, Dawid Migacz, Dawid Paradowski, Andrzej Piasecki, Jakub Ptak, Paweł Sawicki, Krzysztof Sieja, Karol Stanclik, Wojciech Tomiczek, Marzena Wąsiewicz, Marcin Wolak, Piotr Wróbel, Adam Wrzesiński,
• 4 - Dominik Zygmunt,
• 2,5 - Daria Bumażnik, Agata Dziwok, Zuzanna Wołczańska.
  Pozostałe osoby otrzymały 0 punktów ze względu na brak uzasadnienia odpowiedzi.