Początkowo definicja wielościanów półforemnych wymagała tylko, by ich ściany były foremne, a wierzchołki przystające. Nie było w niej warunku wierzchołkowej tranzytywności, czyli istnienia izometrii przekształcającej każdy wierzchołek na każdy inny. Tymczasem nieco ponad 100 lat temu okazało się, że istnieje nieznany dotąd wielościan (ryc. 1) spełniający te pierwsze dwa warunki. Swoim wyglądem bardzo przypomina on sześcio-ośmiościan rombowy mały (ryc. 2). Ściany obu tych wielościanów są trójkątami równobocznymi (jest ich 8) lub kwadratami (6+12), a układ ścian w wierzchołku jest 3-4-4-4. Czym zatem się różnią?
|
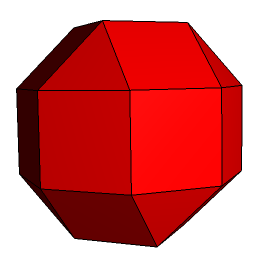
Ryc. 1 pseudo sześcio-ośmiościan rombowy mały |
Ryc. 2 sześcio-ośmiościan rombowy mały |
Zauważmy, że "prawdziwy" sześcio-ośmiościan rombowy mały ma trzy "pasy" złożone z kwadratów. Jego pseudo-bliźniak (nazwany pseudo sześcio-ośmiościanem rombowym małym) taki "pas" ma tylko jeden. Możemy myśleć, że obie bryły składają się z takiego pasa i dwóch "czapeczek" - górnej i dolnej. Jedna bryła powstaje z drugiej w wyniku przekręcenia np. górnej "czapeczki" o 45°. Ta stosunkowo niewielka modyfikacja powoduje, że zupełnie zmieniają się własności całego wielościanu. Sześcio-ośmiościan rombowy mały posiada znacznie więcej symetrii własnych, przez co jawi się jako znacznie bardziej atrakcyjny od swojego "brata". Jeżeli np. sześcio-ośmiościan rombowy mały zamiast na "dolnej" postawimy na "górnej" ścianie, to nikt, kto tego nie widział, nie będzie w stanie rozpoznać, że został on poruszony. W przypadku takiej samej operacji dokonanej na pseudo sześcio-ośmiościanie rombowym małym jego przestawienie będzie wyraźnie widoczne - zmianę położenia zdradzi inne niż pierwotnie ułożenie trójkątów i kwadratów w górnej i dolnej warstwie. Właśnie dlatego, że ta nowa bryła "nie wygląda jednakowo z każdej strony", nie spełnia trzeciego warunku w definicji wielościanu półforemnego.
Omawianą bryłę odkrył wspomniany już J.C.P. Miller, który podobno wykonując model zwykłego sześcio-ośmiościanu rombowego małego pomylił się i źle przykleił jedną z "czapeczek". To, co powstało, spowodowało konieczność uważnego przyjrzenia się definicji półforemności. Matematycy podzielili się. Jedni uznali, że wielościan ten powinien być zaliczony do archimedesowych, inni starali się tak zmodyfikować definicję wielościanu archimedesowego, aby wykluczyć nowoodkrytego dziwaka. Miller i Coxeter (czyli odkrywcy kompletu wielościanów jednorodnych) opowiedzieli się za tą drugą koncepcją - odmówili nowej bryle prawa do bycia półforemną. Spór o jej przynależność do grona wielościanów półforemnych nie został jednak jednoznacznie rozstrzygnięty.
Zupełnie niedawno okazało się, że pseudo sześcio-ośmiościan rombowy mały ma swój odpowiednik wśród wielościanów niewypukłych. W 1994 roku Richard Hughes-Jones opisał nieznany wcześniej wielościan (ryc. 3) powstający przez analogiczne do opisanego wyżej przekręcenie z niewypukłego sześcio-ośmiościanu rombowego wielkiego (ryc. 4). Nowej bryle nadał nazwę pseudo sześcio-ośmiościan rombowy wielki. Jak poprzednio, obie bryły mają 8 ścian trójkątnych i 18 kwadratowych, znowu w wierzchołku każdej z tych brył schodzi się trójkąt i trzy kwadraty, tylko że teraz tworzą one strukturę gwiaździstą.
|
Ryc. 3 pseudo sześcio-ośmiościan rombowy |
Ryc. 4 sześcio-ośmiościan rombowy |
W następnych latach wykazano, że sześcio-ośmiościany rombowe mały i wielki wklęsły są jedynymi wielościanami jednorodnymi posiadającymi swoich niejednorodnych "braci".
Na tym zakończyła się trwająca z górą 2500 lat historia odkrywania wielościanów jednorodnych.
Rysunki wielościanów przedstawione powyżej zostały wyeksportowane z programu Great Stella.
Galeria pseudo wieloscianów jednorodnych
Kliknij, aby powiększyć zdjęcie w osobnym oknie.









 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Super, ale......
Super, ale czy możecie dać tu siatkę sześcio-ośmiościanu rombowego wielkiego niewypukłego i jego pseudo wersji w kilku elementach? Albo przekierować na jakąś stronę internetową o tych dwóch wielościanach?
Już wiem!
Jeśli ktoś chce wykonać model pseudo sześcio-ośmiościanu rombowego małego, może "zmodernizować" sześcio-ośmiościan rombowy mały. A siatkę tego wielościanu można znaleźć w książce W krainie wielościanów.