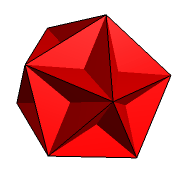
Ściany wielościanów Keplera-Poinsota przenikają się wzajemnie i dlatego też należy poświęcić kilka zdań na omówienie sposobu konstrukcji ich zewnętrznych elementów. W przypadku dwunastościanu gwiaździstego małego (rys. 1) i dwunastościanu gwiaździstego wielkiego (rys. 2) sprawa jest prosta. Ich ścianami są pentagramy, z których na zewnątrz widoczne są tylko ramiona (rys. 3).
Rys. 1 Rys. 2 Rys. 3
Również nietrudno jest skonstruować ścianę dwunastościanu wielkiego (rys. 4). Jest to pięciokąt foremny, z którego na zewnątrz widocznych jest pięć trójkątów równoramiennych (rys. 5).
Rys. 4 Rys. 5
Nieco trudniej skonstruować ścianę dwudziestościanu wielkiego (rys. 6). Kluczem do konstrukcji jest złoty podział. Punkty P oraz Q dzielą krawędź AB w ten sposób, że
AB/AQ=AQ/AP=(1+√5)/2 ≈ 1,618.
Podobnie podzielone są krawędzie BC i AC (rys. 7).
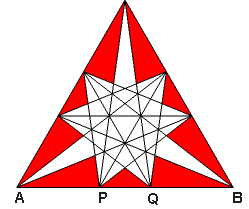
Rys. 6 Rys. 7
Po skonstruowaniu zewnętrznych elementów ścian pozostaje jeszcze takie ich połączenie, aby otrzymany model był odpowiednio sztywny. Kliknięcie w odpowiedni link otwiera w nowym oknie element siatki danego wielościanu Keplera-Poinsota.
dwunastościan gwiaździsty mały (x12)
dwunastościan gwiaździsty wielki (x20)
dwunastościan wielki (x20) Linie przerywane oznaczają krawędzie wklęsłe (zagięcia "do góry").
dwudziestościan wielki (x30) Linie przerywane oznaczają krawędzie wklęsłe (zagięcia "do góry").
W przypadku dwunastościanu gwiaździstego małego i wielkiego elementy siatki są prawidłowymi ostrosłupami. Można je albo połączyć ze sobą używając podwójnych skrzydełek, albo dokleić do wykonanego wcześniej modelu foremnego dwunastościanu (dwunastościan gwiaździsty mały) lub dwudziestościanu (dwunastościan gwiaździsty wielki).
Elementem dwunastościanu wielkiego jest odwrócony ostrosłup trójkątny pozbawiony podstawy. Poszczególne części łączymy tak, by nieistniejące podstawy utworzyły dwudziestościan foremny. W razie wątpliwości można spojrzeć jeszcze raz na rys. 4.
Najbardziej skomlikowana sprawa jest w dwudziestościanem wielkim. W tym wypadku element składa się z dwóch części. Większa niech nazywa się A, mniejsza - B (patrz odpowiedni plik). Część A składa się z czterech trójkątów, których fragmenty są zakreskowane. W ten sposób oznaczone są miejsca, do których dokleić należy część B. Sklejamy obie części A oraz B. Następnie część B wklejamy do części A przyklejając zakreskowane ściany części B do zakreskowanych fragmentów ścian części A. Powstały element można z łatwością odnaleźć na rys. 6. Kolejne elementy łączymy ze sobą za pomocą "długich"skrzydełek części A.
Wizerunki wielościanów zostały wyeksportowane z programu Great Stella. Siatki zostały przygotowane przy użyciu programu Wingeom.
Macie problem?
Jeśli macie problem z dwunastościanem gwiaździstym małym, wydrukujcie to:
http://www.matematyka.wroc.pl/files/u9/archim_dwudziesto-dwunastoscian.g...
lub to: http://www.matematyka.wroc.pl/files/u9/plat_dwunastoscian.gif