stopień trudności:
- trudniejszy przeznaczony dla klas z rozszerzonymi treściami z matematyki
- zadanie z (*) obowiązkowe na ocenę celującą
- grupy A i B mają ten sam stopień trudności
ocenianie:
21-22 - celujący
18-20 - bardzo dobry
15-17 - dobry
11-14 - dostateczny
8-10 - dopuszczający
0-7 - niedostateczny
czas pisania: 45 minut
typ sprawdzianu:
- sprawdzający wiadomości po zakończeniu działu tematycznego, uczeń powinien przedstawić pełny tok rozumowania i obliczenia
- może być wykorzystany jako powtórzenie wiadomości z danego działu przed testem kompetencji
grupa A (22 pkt)
Zad. 1. (6 pkt) Wykresy przedstawiają szacowany stan zasobów ropy naftowej na świecie. Na ich podstawie odpowiedz na pytania.
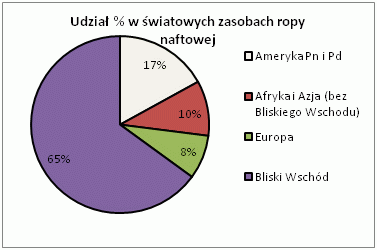
a) Jaką część światowych zasobów ropy naftowej stanowią zasoby Afryki i Azji (bez Bliskiego Wschodu)?
b) Czy to prawda, że zasoby ropy naftowej w obu Amerykach są ponad dwukrotnie większe od zasobów europejskich?
c) Zasoby światowe ropy naftowej ocenia się na 140 mld ton. Ile ton ropy naftowej znajduje się w Afryce i Azji (bez Bliskiego Wschodu)?
d) O ile zasoby europejskiej ropy naftowej są mniejsze od zasobów amerykańskich?
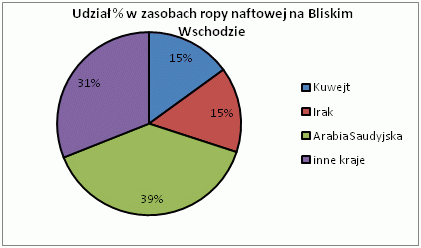
e) Jaki procent światowych zasobów ropy naftowej znajduje się w Arabii Saudyjskiej?
f) Ile ton ropy naftowej znajduje się w Kuwejcie?
Zad. 2. (2 pkt) Dane są liczby: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Skreśl pięć z nich w taki sposób, aby pozostałe spełniały dany warunek.
a) Mediana jest równa średniej arytmetycznej.
b) Mediana jest mniejsza niż średnia arytmetyczna.
Zad. 3. (3 pkt) W klasie 2c aż 28 uczniów nie miało ocen niedostatecznych na półrocze, jeden otrzymał 7 ocen niedostatecznych, inny trzy, dwóch uczniów po dwie i czterech po jednej ocenie niedostatecznej.
a) Przedstaw dane w tabeli.
b) Podaj średnią arytmetyczną, medianę i modę liczby ocen niedostatecznych przypadających na ucznia tej klasy.
Zad. 4. (4 pkt) Tabela przedstawia wyniki pomiarów temperatury ze stacji meteorologicznej w Mysłakowie.
| data | poniedziałek 5.02.12 |
wtorek 7.02.12 |
środa 8.02.12 |
czwartek 9.02.12 |
piątek 10.02.12 |
sobota 11.02.12 |
niedziela 12.02.12 |
| temperatura w °C (6:00) | –18 | –18 | –21 | –19 | –10 | –6 | –3 |
| temperatura w °C (22:00) | –12 | –14 | –16 | –15 | –11 | –5 | –2 |
a) Jaka była średnia arytmetyczna i moda porannych temperatur?
b) Jaki był rozstęp porannych temperatur?
c) Którego dnia różnica między temperaturą poranną i wieczorną była największa?
d) Wykonaj diagram słupkowy pionowy dla porównania temperatur porannych i wieczornych w ciągu tego tygodnia.
Zad. 5. (3 pkt ) Zapisano kolejne wyniki, jakie się zdarzyły w 50-krotnym rzucie kostką do gry.
2 4 3 2 6 5 6 4 1 4
3 6 5 2 1 5 5 4 3 2
6 4 1 3 5 3 5 4 6 1
3 1 1 2 5 6 3 1 3 6
4 3 3 4 6 1 3 1 2 6
a) Wykonaj tabelę częstości wyników.
b) Narysuj procentowy diagram kołowy uzyskanych wyników.
c) Wyznacz modę otrzymanych wyników.
Zad. 6. (4 pkt) Średnią ważoną n liczb a1, a2,…, an, którym przypisano dodatnie wagi w1, w2,…, wn obliczamy według wzoru: [tex]\frac{a_1\cdot w_1+ a_2\cdot w_2 +\ldots + a_n\cdot w_n}{ w_1+ w_2 +\ldots + w_n}[/tex]. W klasie 2a nauczyciel matematyki, wystawiając oceny semestralne i roczne, przypisuje stopniom następujące wagi: ocena za I semestr – 6, testy semestralne i roczne – 5, sprawdzian – 4, odpowiedź – 4, praca na lekcji – 2, aktywność – 3, kartkówka – 3, projekt – 2, praca domowa – 1, a ocenę zaokrągla do pełnych stopni wg tabeli:
| stopień | średnia |
| niedostateczny | poniżej 1,51 |
| dopuszczający | od 1,51 do 2,50 |
| dostateczny | od 2,51 do 3,50 |
| dobry | od 3,51 do 4,50 |
| bardzo dobry | od 4,51 do 5,50 |
| celujący | od 5,51 |
a) Kasia otrzymała za I semestr ocenę bardzo dobrą, a w II semestrze następujące oceny: 4, 3, 2 ze sprawdzianów, 3, 4, 5 z kartkówek, dwie piątki z prac domowych, 6 z projektu, 5 z aktywności, 5 z odpowiedzi i 5 z testu semestralnego. Jaką ocenę roczną otrzyma Kasia?
b*) Czy Janek ma szansę na ocenę bardzo dobrą na I semestr, jeśli dotychczas uzyskał takie stopnie: 4, 5, 6 z kartkówek, 4, 5 ze sprawdzianów, 5 z odpowiedzi ustnej, 4 z pracy domowej, 5 z aktywności, 4 z pracy na lekcji, a przed nim jest jeszcze test semestralny? W jaki sposób test może wpłynąć na jego ocenę semestralną?
grupa B (22 pkt)
Zad. 1. Wykresy przedstawiają szacowany stan zasobów ropy naftowej na świecie. Na ich podstawie odpowiedz na pytania.


a) Jaką część światowych zasobów ropy naftowej stanowią zasoby Europy i obu Ameryk?
b) Czy to prawda, że zasoby ropy naftowej na Bliskim Wschodzie są ponad ośmiokrotnie większe od zasobów europejskich?
c) Zasoby światowe ropy naftowej ocenia się na 140 mld ton. Ile ton ropy naftowej znajduje się na Bliskim Wschodzie?
d) O ile zasoby Afryki i Azji (bez Bliskiego Wschodu) są mniejsze od zasobów amerykańskich?
e) Jaki procent światowych zasobów ropy naftowej znajduje się w Kuwejcie?
f) Ile ton ropy naftowej znajduje się w Arabii Saudyjskiej?
Zad. 2. (2 pkt) Dane są liczby: 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Skreśl pięć z nich w taki sposób, aby pozostałe spełniały podany warunek.
a) Mediana jest równa średniej arytmetycznej.
b) Mediana jest większa niż średnia arytmetyczna.
Zad. 3. (3 pkt) W klasie 2a aż 24 uczniów nie miało ocen niedostatecznych na półrocze, jeden uczeń otrzymał ich 8, inny cztery, dwóch po dwie i czterech po jednej ocenie niedostatecznej.
a) Przedstaw dane w tabeli.
b) Podaj średnią arytmetyczną, medianę i modę liczby ocen niedostatecznych przypadających na ucznia tej klasy.
Zad. 4. (4 pkt) W tabeli przedstawiono wyniki pomiarów temperatury za stacji meteorologicznej w Mysłakowie.
| data | poniedziałek 5.02.12 |
wtorek 7.02.12 |
środa 8.02.12 |
czwartek 9.02.12 |
piątek 10.02.12 |
sobota 11.02.12 |
niedziela 12.02.12 |
| temperatura w °C (6:00) | –18 | –18 | –21 | –19 | –10 | –6 | –3 |
| temperatura w °C (22:00) | –12 | –14 | –16 | –15 | –11 | –5 | –2 |
a) Podaj średnią arytmetyczną i medianę wieczornych temperatur.
b) Podaj rozstęp wieczornych temperatur.
c) Którego dnia różnica między temperaturą poranną i wieczorną była najmniejsza?
d) Wykonaj diagram słupkowy poziomy porównujący tygodniowe temperatury poranne i wieczorne.
Zad. 5. (3 pkt ) Zapisano kolejne wyniki, jakie się zdarzyły w 50-krotnym rzucie kostką do gry.
3 4 3 2 6 5 6 4 6 5
3 6 5 2 1 5 5 4 3 2
6 4 1 3 5 3 5 4 6 1
3 1 1 2 5 6 5 1 6 3
4 3 4 3 6 1 4 1 2 6
a) Wykonaj tabelę częstości wyników.
b) Narysuj procentowy diagram kołowy otrzymanych wyników.
c) Wyznacz modę otrzymanych wyników.
Zad. 6. (4 pkt) Średnią ważoną n liczb a1, a2,…, an, którym przypisano dodatnie wagi w1, w2,…, wn obliczamy według wzoru: [tex]\frac{a_1\cdot w_1+ a_2\cdot w_2 +\ldots + a_n\cdot w_n}{ w_1+ w_2 +\ldots + w_n}[/tex]. W klasie 2c nauczyciel matematyki, wystawiając oceny semestralne i roczne, przypisuje stopniom następujące wagi: ocena za I semestr – 5, testy semestralne i roczne – 5, sprawdzian – 4, odpowiedź – 3, praca na lekcji – 2, aktywność – 3, kartkówka – 3, projekt – 1, praca domowa – 1, a ocenę zaokrągla do pełnych stopni wg tabeli:
| stopień | średnia |
| niedostateczny | poniżej 1,51 |
| dopuszczający | od 1,51 do 2,50 |
| dostateczny | od 2,51 do 3,50 |
| dobry | od 3,51 do 4,50 |
| bardzo dobry | od 4,51 do 5,50 |
| celujący | od 5,51 |
a) Ania otrzymała za I semestr ocenę 4, a w II semestrze następujące oceny: 5, 3, 3 ze sprawdzianów, 6, 5, 5 z kartkówek, dwie piątki z prac domowych, 5 za projekt, 6 za aktywność, 5 z odpowiedzi, 6 z testu semestralnego. Jaką ocenę roczną otrzyma Ania?
b*) Czy Jacek ma szansę na ocenę dostateczną na I semestr, jeśli dotychczas uzyskał: 2, 4 z kartkówek, 4, 2, 3 ze sprawdzianów, 4 z odpowiedzi, 1 z pracy domowej, 3 z aktywności i 1 z pracy na lekcji, a przed nim jest jeszcze test semestralny? W jaki sposób test może wpłynąć na jego ocenę semestralną?
odpowiedzi
grupa A
1. a) 0,1, b) tak, c) 14 mld ton, d) o 12,6 mld ton, e) 25,35%, f) 13,65 mld ton
2. a) np. zostawiamy liczby: 3, 4, 5, 6, 7, b) np. zostawiamy liczby: 1, 2, 3, 8, 9
3. a) tabela poniżej, b) średnia=0,5, mediana=0, moda=0
| liczba ocen ndst | liczba uczniów |
|
0 |
28 4 2 1 1 |
4. a) średnia≈13,57°C, moda=–18°C, b) 18°C, c) w poniedziałek 6°C, d) wykres poniżej
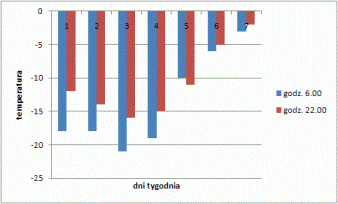
5. a)- b) tabela poniżej, c) moda=3
| liczba oczek | częstość | kąt środkowy w diagramie kołowym w stopniach |
|
1 |
0,18 0,12 0,22 0,16 0,14 0,18 |
64,8 43,2 79,2 57,6 50,4 64,8 |
6. a) średnia≈4,28, ocena=dobry b) Jeżeli otrzyma 4, 5 lub 6 będzie miał na semestr bardzo dobry. Jeśli otrzyma 1, 2 lub 3 - dobry.
grupa B
1. a) 0,25, b) tak, c) 91 mld ton, d) o 9,8 mld ton, e) 9,75%, f) 35,49 mld ton
2. a) np. zostawiamy liczby: 8, 9, 10, 11, 12, b) np. zostawiamy liczby: 3, 4, 10, 11, 12
3. a) tabela poniżej, b) średnia=0,625, mediana= 0, moda=0
| liczba ocen ndst | liczba uczniów |
|
0 |
24 4 2 1 1 |
4. a) średnia≈10,71°C, mediana=–12°C, b) 14°C, c) w piątek, sobotę, niedzielę 6°C, d) wykres poniżej
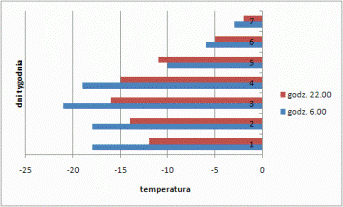
5. a)- b) tabela poniżej, c) moda=3
| liczba oczek | częstość | kąt środkowy w diagramie kołowym w ° |
|
1 |
0,16 |
57,6 |
6. a) średnia=3,6, ocena - dobry, b) Jeżeli otrzyma 3, 4, 5 lub 6 będzie miał na semestr - dostateczny. Jeśli otrzyma 1 lub 2 - dopuszczający.
kryteria oceniania
1. a)- e) po 1 punkcie za odpowiedź
2. a)- b) po 1 punkcie za odpowiedź z uzasadnieniem
3. a) 1 pkt za tabelę b) 1 pkt za średnią, po 0,5 pkt za medianę i modę
4. a)- d) po 1 punkcie
5. a)- c) po 1 punkcie
6. a) 1 pkt za zapisanie wyrażenia arytmetycznego do obliczenia średniej ważonej, 1 pkt za obliczenie średniej i podanie stopnia b) 1 pkt za nierówność, 1 pkt za rozwiązanie nierówności i podanie odpowiedzi

 Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć? Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
 Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera.
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 

