| więcej informacji o tekście: |
2015-08-25
Nieziemskie przyciąganie (przeskalowanie) jest kolejnym przykładem omyłkowego przekształcenia (porównaj z Omyłkowe przekształcenia - emsymetria i Omyłkowe przekształcenia - orsymetria>). Omówimy własności tego odwzorowania. Będzie to podsumowanie do tekstu Nieziemskie przyciąganie - zadania, który koniecznie należy przeczytać wcześniej.
1. Określenie przekształcenia
Dla figury (domkniętej) wypukłej c, punktu Z i liczby s >0 określamy:
Zc = punkt z c leżący najbliżej Z,
Z' = punkt z półprostej ZcZ taki, że
ZcZ' = s . ZcZ .
Ponadto dla figury u symbol u' = Pcs ( u ) oznacza nową figurę utworzoną z punktów Z', dla Z z u.
Będziemy mówić, że figura u jest (nieziemsko) przyciągana przez centrum c w skali s, albo że u' jest obrazem figury u w przekształceniu Pcs.
Poniżej widać efekt działania przekształcenia Pcs dla różnych wielokątów (można zmieniać położenia wierzchołków i całych figur).
2. Obrazy odcinków
Kluczem do zrozumienia tego przekształcenia jest zbadanie, co jest w nim obrazem odcinka oraz w których miejscach obraz odcinka 'załamuje się'.
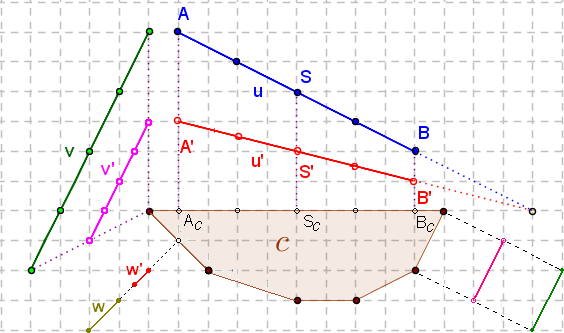
Na poniższym rysunku, przy skali s=1/2 widać ilustrację ogólnej tezy:
Obserwacja 1. Gdy wszystkie punkty odcinka v są przyciągane przez ten sam wierzchołek z centrum c (tzn. gdy dla wszystkich punktów z v wierzchołek z centrum c leży do nich najbliżej), to
a) obraz v' odcinka v jest odcinkiem,
b) długość v' = s . długość v ,
c) v' jest równoległy do v .
Widać też tezę nieco ogólniejszą:
Obserwacja 1'. Gdy wszystkie punkty odcinka v są przyciągane przez ten sam punkt z centrum c, to
a) obraz v' odcinka v jest odcinkiem,
b) długość v' = s . długość v ,
c) v' jest równoległy do v.
Dla innych odcinków, takich jak u na powyższym rysunku, mamy:
Obserwacja 2. Gdy końce A i B odcinka u są przyciągane przez różne punkty z tego samego boku centrum c, to obraz u' odcinka u jest odcinkiem o końcach A' i B'.
Uwaga 1. Dowód powyższych obserwacji może być oparty na podobieństwie trójkątów lub na twierdzeniu Talesa.
Dla dowolnego odcinka jego obraz jest łamaną. Wyznaczenie tej łamanej nie jest trudne, choć bywa żmudne. Pomocne jest zaznaczenie prostych prostopadłych do boków centrum c wystawionych w jego wierzchołkach.
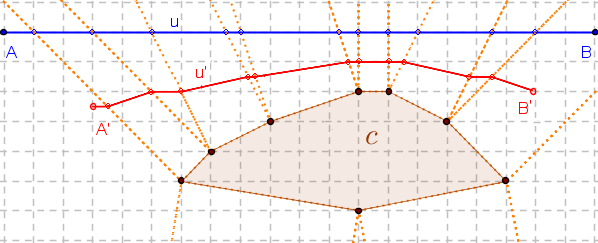
Uwaga 2. Wydaje się, że ogólnie zachodzi warunek:
leżą na prostych prostopadłych do boków centrum c wystawionych w jego wierzchołkach.
3. Pola obrazów figur
Zobaczmy, jak zmienia się pole figury w tym przekształceniu.
Zależy to od położenia figury.
Przeanalizujmy prosty przykład.
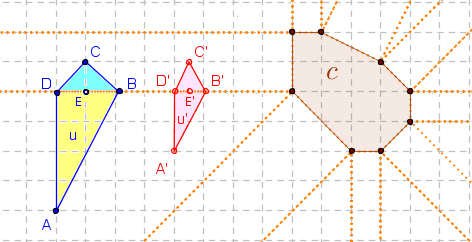
pole u' = pole D'B'C' + pole D'B'A'
=
1/2 . D'B' . E'C'
+
1/2 . D'B' . D'A'
=
=
1/2 . (1/2 . DB)
. EC
+
1/2 . (1/2 . DB) . (1/2 . DA)
=
=
1/2 . (1/2 . DB
. EC )
+
1/2 . 1/2 . (1/2 . DB . DA)
=
=
1/2 . pole DBC
+
1/2 . 1/2 . pole DBA
=
=
s . pole
DBC
+
s2 . pole
DBA .
Widać, że inaczej zmienia się część 'niebieska', a inaczej - część 'żółta' figury.
Dla wielokątów widać algorytm postępowania.
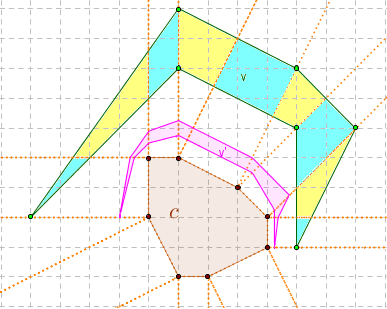
pole v'
=
s .
pole
części niebieskiej
+
s2 . pole
części żółtej
=
=
1/4 .
9 89/140 +
(1/4)2 .
9 51/140
=
2 2227/2240
.
Dla figury, której pole możemy przybliżać polami wielokątów, możemy postępować podobnie:
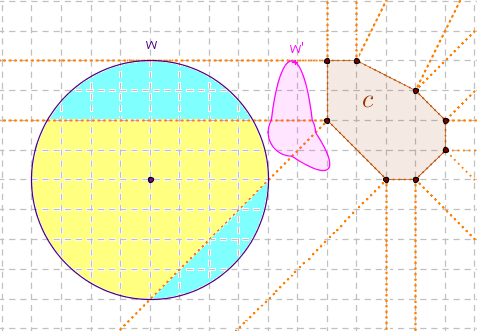
pole w'
=
s .
pole
części niebieskiej
+
s2 . pole
części żółtej
=
=
s .
(
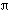28/3 - 8 - 8
)
+
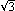s2 .
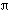( 20/3 + 8 + 8).
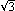Odnotujmy, że w powyższym przykładzie obrazem okręgu ograniczającego w jest linia złożona z dwóch fragmentów elips i dwóch łuków okręgu.
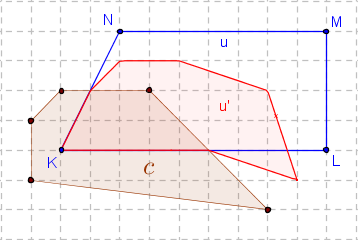Uwaga 3. Może wydawać się, że ów kolorowy wzór na pole przekształconej figury jest całkiem ogólny. Tak jednak nie jest.
Podzielenie figury na części 'niebieską' i 'żółtą' nie wystarcza.
Obok pokazano, że trzeba też uwzględnić trzecią część - zawartą w centrum c.
Na tym rysunku widać również, że obrazem odcinka KL jest łamana o jednym z wierzchołków leżącym poza prostymi prostopadłymi w wierzchołkach do boków c.
uc składa się z punktów u leżących w c ,
uw składa się z punktów u 'przyciąganych' przez wierzchołki c ,
ub składa się z pozostałych punktów u,
to
4. Składanie przekształceń
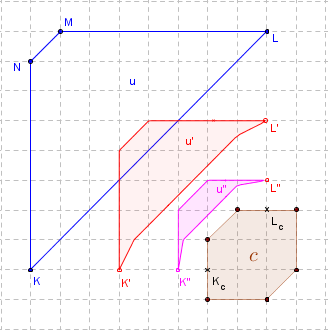Na rysunku obok figurę u najpierw przekształcono przez
Pc1/2. Efekt u' tego przekształcenia poddano kolejnemu przekształceniu
Pc1/3, otrzymując w wyniku u''.
Łatwo można sprawdzić, że u'' jest obrazem u w
jednym przekształceniu Pc1/6.
Symbolicznie:
Tak jest ogólnie.
Niemal natychmiastowo wyciągamy następujące wnioski:
a) Pc1 ( Z ) = Z, czyli przekształcenie Pc1 nic nie zmienia (jest identycznością).
b') Jeśli Z' = Pc1/2 (Z), to Pc2 (Z') = Z , czyli przekształcenie Pc2 jest odwrotne do Pc1/2.
b) Jeśli Z' = Pcs (Z), to Pc1/s (Z') = Z , czyli przekształcenie Pc1/s jest odwrotne do Pcs.
c) Pct (Pcs (Z)) = Pcs (Pct (Z)), czyli składanie przekształceń: Pcs i Pct jest przemienne.
Uwaga 5. Może się wydawać, że te przekształcenia nie zmniejszą liczby boków wielokątów.
Tak nie jest. Oto prosty argument:
jeśli u' = Pcs (u) ma więcej boków niż u, to
Pc1/s (u') = u ma mniej boków niż u'.
5. Wklęsłe centrum
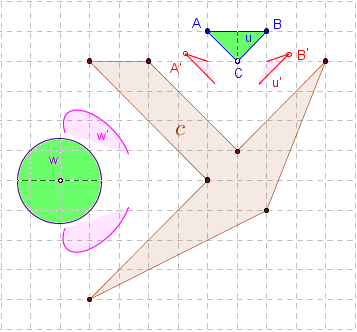Obok pokazano, co się dzieje, gdy centrum c nie jest wypukłe.
Obrazy figur mogą być wtedy 'rozerwane'. Powodem jest brak jednoznaczności najbliższego punktu, mianowicie są punkty z v, dla których istnieje więcej niż jeden najbliższy punkt z c.
'Lekarstwem' (dość często stosowanym w matematyce) jest wówczas wyrzucenie tych 'złych' punktów (tzn. tych, dla których istnieje więcej niż jeden najbliższy punkt z c) z dziedziny przekształcenia Pcs.
Zatem dla c z rysunku obok, punkty z linii przerywanych nie są przekształcane. Dziedziną Pcs jest płaszczyzna bez punktów dwóch półprostych.
Przy takiej umowie co do dziedziny, można rozważać również przekształcenia Pcs dla zbiorów c, które nie są figurami wypukłymi. Poniżej c jest brzegiem czworokąta. Proszę sprawdzić, jaka jest dziedzina tego przekształcenia i które z wcześniejszych obserwacji pozostają prawdziwe. Ciekawy jest też zbiór wartości tego przekształcenia (figura złożona z tych i tylko tych punktów płaszczyzny, które są obrazami punktów w tym przekształceniu).
6. Centrum okręgiem
Ciekawy jest przykład przekształcenia Pcs dla c będącego okręgiem. Proszę sprawdzić, jaka jest dziedzina tego przekształcenia i które z wcześniejszych obserwacji pozostają prawdziwe.
Uwaga 6. Dla dla c będącego okręgiem, obrazami odcinków są (na ogół) fragmenty linii zwanych konchoidami prostej (przedłużenie odcinka AB), a obrazami okręgów są linie zwane konchoidami okręgów.
7. Skala ujemna?
W określeniu przekształcenia Z' = Pcs (Z) podano, że
Z' = punkt z półprostej ZcZ taki, że
ZcZ' = s . ZcZ .
Jak interpretować taki zapis dla s < 0?
Gdyby traktować półprostą ZcZ jako półoś liczbową, to zapis ZcZ' = s . ZcZ można odczytać, jako określenie punktu Z' leżącego na uzupełnieniu tej półprostej, w odległości |s| . ZcZ
od Zc.
(Najwygodniej można zapisać to wektorami, czego tu czynić nie będziemy.)
Skala s = -1 oznacza jakby odbicie względem c.
Gdy c jest punktem, to Pc-1 jest odbiciem względem punktu (tzn. symetrią środkową, czyli obrotem o 180o).
Gdy c jest prostą, to Pc-1 jest odbiciem względem prostej (czyli symetrią osiową).
Dla c będącego okręgiem lub brzegiem czworokąta, ostatnie dwa dynamiczne rysunki pokazują efekt takiego przekształcenia również przy s < 0.
Tylko część poprzednich obserwacji zachodzi przy s < 0. Warto zastanowić się dlaczego.
O przekształceniu Pc-1 pisaliśmy już wcześniej w innych artykułach. Wtedy nosiło ono inne (wymyślne) nazwy:
Omyłkowe przekształcenie - emsymetria - gdy c było łamaną,
Omyłkowe przekształcenie - orsymetria - gdy c było okręgiem,
Omyłkowe przekształcenie - parsymetria - gdy c było parabolą.
8. Skala s = 0 ???
Co dzieje się w przypadku s = 0?
Wskazówka.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
