|
Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą. |
W tekstach Światowidy dyskretne oraz Światowidy wielościenne pokazaliśmy najprostsze bryły, które oglądane z profilu i en face wyglądają jednakowo. Przeczytaj koniecznie te artykuły. Teraz pokażemy światowidy, których projekty zadane są przez wykresy funkcji.
Dokładniej: dla funkcji f, określonej na przedziale [0,1], o wartościach nieujemnych, niech P oznacza obszar pomiędzy wykresem f a przedziałem [0,1] osi OX. Bryłę nazwiemy f-światowidem, gdy P jest jej rzutem na płaszczyznę OXZ oraz na płaszczyznę OYZ i gdy jest to największa bryła o tej własności.
Precyzyjne określenie f-światowida nie jest zbyt pasjonujące:
f-światowidem nazywamy zbiór { (x,y,z): 0
z
min(f(x), f(y)) } .
Ciekawsze jest wyznaczanie objętości f-światowidów.
Podamy tu kilka przykładów (bez ogólnego wzoru),
w których wygodnie jest zastosować poniższe ogólne twierdzenie:
(*) Reguła Cavalieriego.
Niech dane będą dwie bryły B1 i B2 i ustalona płaszczyzna
K.
Jeśli dla każdej płaszczyzny L równoległej do K, przekroje:
L 
B1
i L B2 mają jednakowe pola,
to objętości brył B1, B2 są jednakowe.
Zobaczmy jak można obliczyć objętość f-światowida dla
to znaczy, gdy wykres funkcji f jest półokręgiem
(i obszar P pod wykresem f jest półkolem).
Zauważmy, że przekroje tego f-światowida płaszczyznami równoległymi do płaszczyzny OXY
są kwadratami. Dla takiej płaszczyzny L, przechodzącej przez punkt (0,0, z), gdzie
0<z<1/2, bok kwadratu przekroju ma długość
(wyznacz z równania 
wielkość |x-0,5| ).
Zatem przekrój ma pole 4(0,25-z^2) = 1 - (2z)^2.
Takie same pole ma przekrój płaszczyzną L bryły B, która jest
różnicą prostopadłościanu o wierzchołkach:
Uwaga. O tej bryle pisaliśmy już w artykule Baryłka Archimedesa.
Zobaczmy jak można obliczyć objętość f-światowida dla f(x) = 4x(1-x).
W tym przykładzie również przekroje f-światowida płaszczyznami równoległymi do płaszczyzny OXY
są kwadratami. Dla takiej płaszczyzny L, przechodzącej przez punkt (0,0, z), gdzie
0<z<1, bok kwadratu przekroju ma długość
(dlaczego?).
Zatem przekrój ma pole 1-z.
Takie same pole ma przekrój płaszczyzną L graniastosłupa B o wierzchołkach:
Zatem, na podstawie (*), objętość tego f-światowida jest równa objętości bryły B, czyli 1/2.
Zobaczmy jak można obliczyć objętość f-światowida dla
.
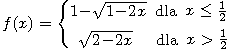W tym przykładzie również przekroje f-światowida płaszczyznami równoległymi do płaszczyzny OXY
są kwadratami. Dla takiej płaszczyzny L, przechodzącej przez punkt (0,0, z), gdzie
0<z<1, bok kwadratu przekroju ma długość 1-z (dlaczego?).
Zatem przekrój ma pole (1-z)2.
Takie same pole ma przekrój płaszczyzną L ostrosłupa B o wierzchołkach:
Dla f-światowida, gdzie
,
objętość jest równa obliczyć 
,
co można uzasadnić metodami wyższej matematyki.
Tą samą objętość mają f-światowidy dla
,
,
.
Zauważmy, że wykres funkcji
,
powstaje z wykresu
,
ten ostatni trzeba
trzykrotnie 'ścisnąć wzdłuż osi OX'. Okresowość powoduje, że na przedziale [0,1]
obie te funkcje mają jednakowe długości przekrojów wzdłuż prostych równoległych
do osi OX.
W konsekwencji przekroje odpowiadających im f-światowidów płaszczyznami
równoległymi do płaszczyzny OXY mają jednakowe pola.
Zatem, na podstawie (*), objętości tych f-światowidów są równe.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
