| więcej informacji o tekście: |
Karuzela - koło młyńskie o promieniu R - kręci krzesełkami, to w górę, to w dół. Siedzisko krzesełka jest kołem o promieniu r. To koło wymiata w przestrzeni pewną bryłę.
Co to za bryła? Zobaczymy poniżej.
Na wstępie zauważmy, że środek siedziska, jak każdy punkt tego koła, kręci się po okręgu o promieniu R (dlaczego?).
Na początek pomyślmy o pewnym uproszczeniu tej karuzeli. Zamiast kręcić krzesełkami, karuzela przesuwa je wzdłuż obwodu kwadratu (wpisanego w koło o promieniu R). Teraz każdy punkt krzesełka 'zatacza' brzeg kwadratu.
[Zwiększ T, zobaczysz wymiataną linię.]
Można przesuwać suwaki i 'wypełnione' punkty.
Uprośćmy też krzesełko, niech będzie odcinkiem o długości 2r.
Jaką powierzchnię wymiata ten odcinek? Jakie jest pole tej powierzchni?
Łatwo podać odpowiedź, gdy kąt
![]() = 90o.
= 90o.
Trochę trudniej, gdy
![]() = 0o.
= 0o.
A jak jest dla ![]() = 45o ?
= 45o ?
[Zwiększ T do 1, zobaczysz 'całą' powierzchnię. Warto też popatrzeć 'z góry'.]
Można przesuwać suwaki i 'wypełnione' punkty.
Niech teraz krzesełko będzie kwadratem (wpisanym w koło o promieniu r).
Jaką bryłę wymiata ten kwadrat? Jaka jest objętość tej bryły? Jakie jest jej pole powierzchni?
Łatwo podać odpowiedź, gdy kąt
![]() = 45o.
= 45o.
Trochę trudniej, gdy
![]() = 0o.
= 0o.
Można przesuwać suwaki i 'wypełnione' punkty.
Niech teraz krzesełko będzie trójkątem równobocznym (wpisanym w koło o promieniu r).
Jaką bryłę wymiata ten trójkąt? Jaka jest objętość tej bryły?
Widać, że najważniejsze jest zrozumienie, jak nachodzą na siebie dwie części tej bryły.
Zbadaj przypadek ![]() = 0o.
= 0o.
Można przesuwać suwaki i 'wypełnione' punkty.
Powróćmy do karuzeli w kształcie koła (o promieniu R).
Kwadratowe krzesełko, ustawione jak na rysunku (![]() = 45o),
wymiata bryłę, którą można od biedy nazwać walcem. Jaka jest jego podstawa?
= 45o),
wymiata bryłę, którą można od biedy nazwać walcem. Jaka jest jego podstawa?
(Obliczenie pola powierzchni tej podstawy wymaga znajomości trygonometrii.)
Można przesuwać suwaki i 'wypełnione' punkty.
Obracając kwadratowe krzesełko, dostajemy jeszcze trudniejsze i ciekawsze bryły.
Gdy r = R i ![]() = 0o,
to znika dziura w środku. Zostaje tylko wgłębienie. Jaki ma kształt?
= 0o,
to znika dziura w środku. Zostaje tylko wgłębienie. Jaki ma kształt?
Można przesuwać suwaki i 'wypełnione' punkty.
Gdy krzesełko jest okręgiem o promieniu r (nie kołem), to wymiata pewną powierzchnię. Powierzchnia ta jest zamknięta, ma dwie zasklepione części. Z góry i z dołu powstają lejki.
To nie są normalne lejki, nie są bryłami obrotowymi.
Można przesuwać suwaki i 'wypełnione' punkty.



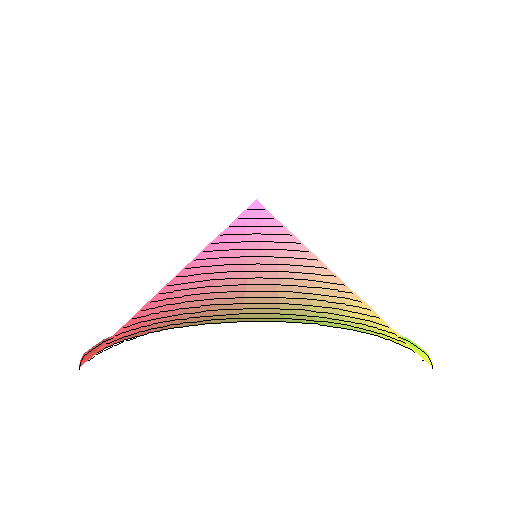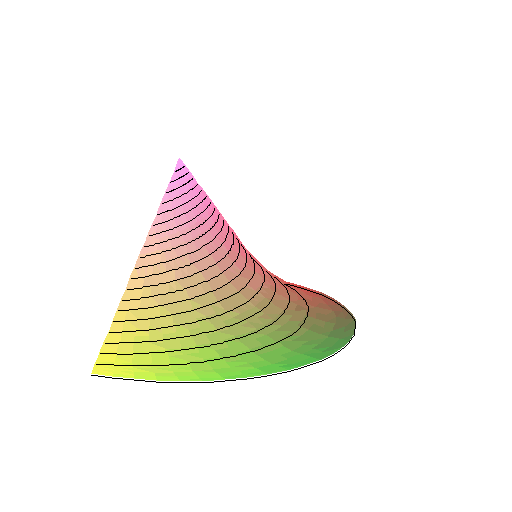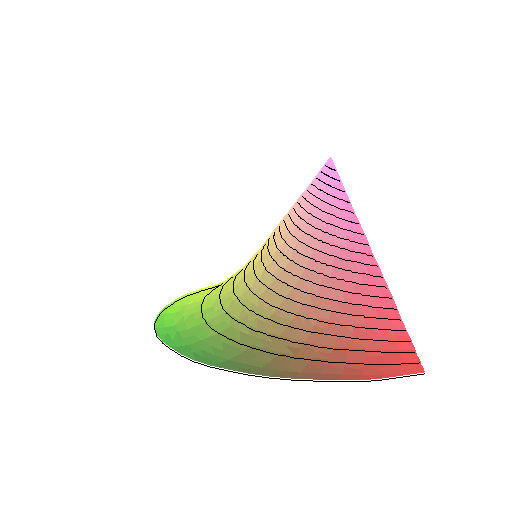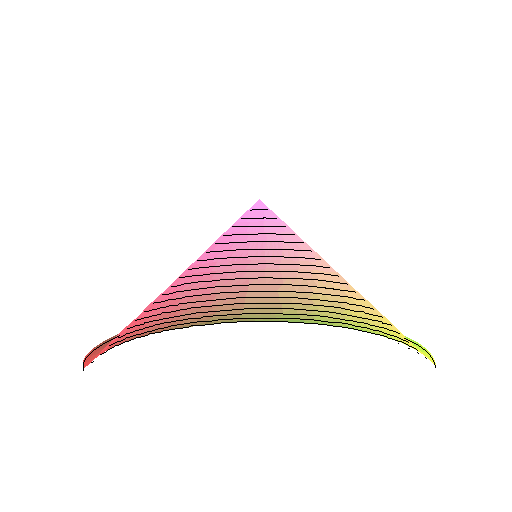



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
