| więcej informacji o tekście: |

zoom |
Kot na ekranie to nic innego jak kolekcja zamalowanych kwadratów (pikseli). W powiększeniu widać to wyraźnie - wypróbuj na rysunku obok. Jak kodować takie obrazki? Tym zajmiemy się poniżej.
Dla ułatwienia ograniczymy się do wersji czarno-białej i na początek rozważać będziemy ekrany o bardzo małej rozdzielczości (4×4).
Biało-czarny obrazek na 16 kratkach (pikselach) można zakodować binarnie (tzn. używając dwóch symboli):
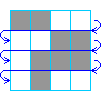
c c b b b b c c b c c c b c b b
Wypisujemy po kolei kolory poszczególnych kratek (b - białe, c - czarne).
To najprostszy sposób kodowania.
Inny sposób kodowania, zwany metodą RLE (Run Length Encoding), ilustrują przykłady:
|
|
|
W metodzie RLE kody są różnej długości. Powiemy, że pierwszy ma długość 16 (8 par: liczba i litera),
kod 5c 6b 5c ma długość 6, a kod 12b 4c ma długość 4.
Uwaga! W długości kodu nie zliczamy cyfr, tylko liczby.
| K O D O W N I K 4×4 (klikając, zmienisz zaczernienie pól) długość kodu = 12 |
Ćwiczenie 1.
Podaj kody i ich długości:
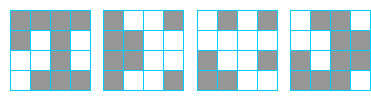
Ćwiczenie 2.
Podaj kody i ich długości:
a) biały kwadrat z jedną czarną przekątną,
b) biały kwadrat z dwoma przekątnymi,
c) zaczerniony obwód kwadratu.
Ćwiczenie 3. Jakie kody są najkrótsze? Wypisz je wszystkie.
Ćwiczenie 4. Jakie kody są najdłuższe? Wypisz je wszystkie.
Ćwiczenie 5. Wypisz wszystkie kody długości 4.
Dość trudno wypisać wszystkie kody długości 6 - jest ich sporo.
Spróbuj zacząć je wypisywać.
Widać, że trudność sprawia zadbanie o to, by wypisać je wszystkie i by żadne kody się nie powtarzały.
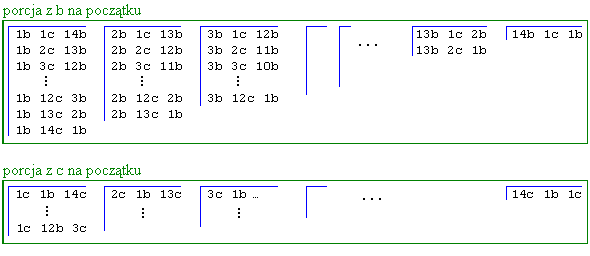
Można to zrobić schematycznie,
na przykład tak
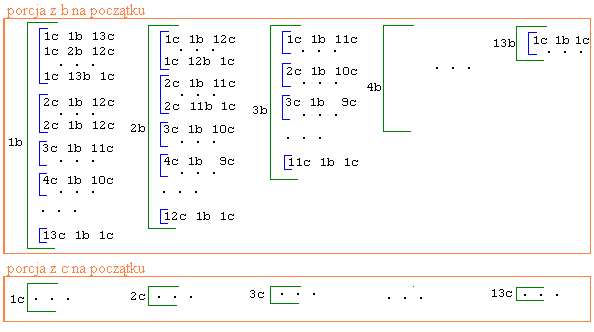
Podobnie schematycznie można przedstawić wszystkie kody długości 8.
(Nim klikniesz, spróbuj zrobić to samodzielnie.)
Na przykład tak
Uwaga! Chyba jest już jasne, że zamiast o kodach obrazka 4×4 można myśleć o kodach paska złożonego z 16 kwadratów:
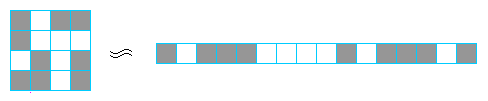
1c 1b 3c 4b 1c 1b 3c 1b 1c
Metoda RLE jest nieco bardziej skomplikowana niż kodowanie binarne.
Dla niektórych obrazków kod RLE jest dłuższy (nawet dwa razy dłuższy), a dla innych krótszy od kodu binarnego, w którym kod każdego obrazka ma długość 16 (na ekranie 4×4).
Czy jest 'opłacalne' stosowanie tego bardziej skomplikowanego sposobu kodowania? Jak zmierzyć tę 'opłacalność'?
Można ją zmierzyć porównując średnią długość kodu w obu sposobach kodowania.
W sposobie binarnym jest równa 16, a w metodzie RLE?
Twierdzenie 1. Dla obrazków złożonych z 16 kwadratów.
W metodzie RLE średnia długość kodu jest równa 17.
Ogólnie jest podobnie.
Twierdzenie 1'. Dla obrazków złożonych z n kwadratów.
W metodzie RLE średnia długość kodu jest równa n + 1.
Zatem metoda RLE jest w pewnym sensie gorsza niż metoda binarna.
Kod losowo wybranego obrazka-paska będzie średnio o jeden dłuższy niż kod binarny. Nasuwa się naturalne pytanie:
Dlaczego więc stosuje się metodę RLE?
Można odpowiedzieć tak:
obrazki zrobione 'ręką' człowieka nie są losowe, grafiki mają na ogół bardzo dużo obszarów tego samego koloru. Wtedy kod RLE jest istotnie krótszy. Inaczej jest w przypadku zdjęć - wtedy nie warto stosować tej metody.
| K O D O W N I K 5×5 (klikając, zmienisz zaczernienie pól) długość kodu = 18 |
Zobaczmy jeszcze pewną modyfikację zapisu metody RLE, na przykładzie obrazków na ekranie 5×5 (patrz obok).
Ćwiczenie 8.
Podaj kody i ich długości:
a) biały kwadrat z jedną czarną przekątną,
b) biały kwadrat z dwoma przekątnymi,
c) zaczerniony obwód kwadratu.
Ćwiczenie 9. Jakie kody są najkrótsze? Wypisz je wszystkie.
Ćwiczenie 10.
Jakie kody są najdłuższe? Wypisz je wszystkie.
Kody niektórych obrazków są bardzo regularne, nasuwa się pomysł, by je upraszczać, by zapisywać je tak, jakby to było potęgowanie, na przykład tak:
c4 b3 c2 b3 c2 b3 c2
b3
c2 b1
=
c4 ( b3 c2 )4 b1 ,
c4 b3 c2 b3 c2 b3 c2
b3
c2 b1
=
c3 ( c1 b3 c1 )4 c1 b1 ,
c1 b2 c2 b3
c1 b2 c2 b3
c1 b2 c2 b3
c1
=
( c1 b2 c2 b3 )3 c1 ,
b1
c1 b2 c1 b2 c1 b2 c3
c1 b2 c1 b2 c1 b2 c3
=
b1 ( ( c1 b2 )3 c3 )2 ,
Tak można bardzo prosto zakodować szachownicę: b1 ( c1 b1 )12
i inne 'rytmiczne' obrazki (przy czym trzeba pamiętać, że nie wolno stosować przemienności mnożenia!).
Nie jest to już metoda RLE ale 'przygrywka' do innych metod kodowania, takich jak LZ (skrót od nazwisk autorów: A. Lempel, J. Ziv). Wykracza to jednak poza ramy tego wstępnego artykułu.
Literatura
A. Drozdek, Wprowadzenie do kompresji danych, WNT, Warszawa 1999 r.



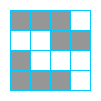
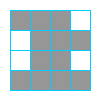
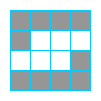
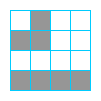
 Ćwiczenie 6 Opisz miejsce, gdzie powyżej jest kod
5b 7c 4b .
Ćwiczenie 6 Opisz miejsce, gdzie powyżej jest kod
5b 7c 4b .
 Ćwiczenie 7 Opisz miejsce, gdzie powyżej jest kod
5c 4b 3c 4b .
Ćwiczenie 7 Opisz miejsce, gdzie powyżej jest kod
5c 4b 3c 4b .
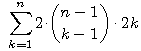 ,
,
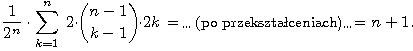





 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
