Czy to prawda, że Mozart był najlepszym matematykiem wśród muzyków? Trudno rozstrzygnąć, ale z pewnością związki jego twórczości z matematyką są głębokie i nieprzypadkowe. Był niezaprzeczalnie wielkim wirtuozem geniuszem muzycznym, który choć żył krótko, pozostawili po sobie wspaniałe dzieła mające duży wpływ na pokolenia przyszłych kompozytorów. Wraz z Haydnem i Beethovenem jest zaliczany do trójki wielkich klasyków wiedeńskich.

Urodził się 27 stycznia 1756 roku w Salzburgu (Austria), zmarł w Wiedniu w wieku 35 lat. Był siódmym dzieckiem Leopolda Mozarta oraz Anny Marii z domu Pertl (ale tylko dwójka rodzeństwa przeżyła okres dziecięcy). Na chrzcie nadano mu imiona Joannes Chrysostomus Wolfgangus Theophilus - pierwsze dwa na cześć patrona dnia urodzin Jana Chryzostoma, Wolfgang - na pamiątkę dziadka ze strony matki, a Teofil - na pamiątkę ojca chrzestnego. Przez większość życia kompozytor posługiwał się jednak imionami Wolfgang i Amadé lub Amadeo (to drugie imię jest francuską/włoską wersją greckiego imienia Teofil i oznacza umiłowany przez Boga), a we wczesnym dzieciństwie występował też jako Wolfgang Gottlieb (to z kolei niemiecki wariant imienia Teofil). Wiadomo, że rodzice wołali nań zdrobniale Wolferl, Wolfgangerl lub Wolfi, do historii przeszedł zaś pod łacińską wersją imienia - Amadeus - której zresztą nigdy nie używał.
Miał starszą o pięć lat siostrę Marię Annę zwaną Nannerl, która także przejawiała uzdolnienia muzyczne. Gdy miała 11 lat, mały Wolfgang grywał z nią duety klawesynowe, choć już w wieku 3 lat zabawiał się wyszukiwaniem tercji na tym instrumencie, a od 5 roku życia zaczął pobierać lekcje gry u swojego ojca i wtedy skomponował swój pierwszy utwór – Menuet i Trio. Jego pamięć muzyczna była fascynująca. Jako 13-latek potrafił bezbłędnie zapisać z pamięci 9-głosowe Miserere Gregoria Allegriego po jednorazowym wysłuchaniu go w Kaplicy Sykstyńskiej (utwór ten przeznaczony był do wykonywania raz w roku, w Wielki Piątek, wyłącznie w tym miejscu; rękopis utworu był przechowywany w archiwum Kaplicy i pod groźbą ekskomuniki nie wolno było go wynosić, kopiować, ani rozpowszechniać).

Koncert małego Mozarta przed cesarzową Marią Teresą (Austrian Archives CORBIS)
Po dziś dzień należy do najbardziej złożonych zjawisk w historii, a wokół niej narosło wiele legend i kontrowersji. Mimo że Mozart umarł młodo, zdążył napisać bez mała 700 niezwykle oryginalnych utworów, często tak monumentalnych jak opery, oratoria, koncerty i symfonie. Jego twórczość wielbiło wielu kompozytorów, nazywano ją bramą do krainy aniołów. Beethoven mawiał, że nigdy nie byłby w stanie stworzyć melodii tak pięknej, jak pierwsze takty 24. koncertu fortepianowego Mozarta. Złożył mu swoisty hołd, pisząc wariacje oparte na jego tematach. Podobne wariacje pisali też Fryderyk Chopin i Gioacchino Rossini. Piotr Czajkowski napisał suitę Mozartiana, Antoni Dworzak porównywał Mozarta do Słońca, a Gustaw Mahler umarł podobno ze słowem Mozart na ustach. Z kolei amerykański krytyk muzyczny Jim Svejda, wypełniając podanie o pracę, w rubryce 'religia' napisał Mozart. Hołd muzyce Mozarta oddawali też przedstawiciele innych dyscyplin: szwajcarski filozof Henri Amiel napisał, że bilans całości utworów Mozarta jest doskonały, niemiecki pedagog muzyczny Hanns Dennerlein opisał twórczość Mozarta jako najdoskonalszą proporcję, angielski muzykolog Eric Blom stwierdził, że Mozart miał nieomylny smak i wiedział dokładnie kiedy i jak długo ma trwać dana część utworu, a Albert Einstein postrzegał muzykę Mozarta jako tak czystą i piękną, że widział w niej odbicie wewnętrznego piękna wszechświata. To właśnie o niej oraz o odkrytej przez siebie teorii względności mawiał, że istniały od zawsze i tylko czekały na ich odkrycie.
Nikt nie wie tak naprawdę, w jaki sposób Mozart tworzył swoje wielkie dzieła i co stanowiło źródła jego inspiracji. Do dziś wielu badaczy analizuje dokładnie jego twórczość, zarówno pod kątem muzyczno-artystycznym jak i matematyczno-logicznym. Badane są występujące w niej relacje, symetrie i ich złożenia, proporcje, harmonie czy permutacje.
Czy rzeczywiście w swojej twórczości Mozart kierował się zasadami matematycznymi? Tego się pewnie nigdy nie dowiemy, ale na pewno wiadomo, że żywo interesował się matematyką i to nie może być kwestią przypadku, że w jego muzyce jest tyle matematycznych zależności.
Siostra Amadeusza opowiadała, że gdy uczył się matematyki, wszystkie meble w domu, ściany i podłoga, były pokryte liczbami, nie myślał i nie rozmawiał wówczas o niczym innym jak tylko o liczbach. Mając 14 lat, pisał do siostry z podróży po Europie, aby wysłała mu jego ćwiczenia z arytmetyki. Alfred Einstein - jeden z biografów Mozarta (daleki kuzyn Alberta) - pisał, że liczby towarzyszyły w pracy Wolfgangowi przez całe życie, na marginesie swoich kompozycji zapisywał równania matematyczne, a na egzemplarzu Fantazji i Fugi C-dur obliczał szanse wygrania na loterii (mimo że sporo zarabiał, w artystycznych kręgach wiedeńskich słynął z zamiłowania do hulaszczych zabaw, co go słono kosztowało, podobnie jak późniejsze wydatki na leczenie żony).
Mozart uwielbiał zagadki logiczne. Bardzo podobała mu się anegdota o wynalezieniu gry w szachy, w której perski uczony Sissa-Nassir poprosił zachwyconego nową grą władcę Indii, aby wynagrodził go taką ilością zboża, jaka znajdzie się na szachownicy, jeśli na pierwszym polu położy jedno ziarenko, a na pozostałych - podwojoną liczbę z pola poprzedniego. Okazało się, że władca mimo posiadanych bogactw, nie był w stanie takiego honorarium wypłacić, gdyż szukana liczba ziaren będąca sumą szeregu geometrycznego złożonego z potęg dwójki o wykładnikach od 0 do 63, wynosi 18 446 774 073 709 551 615. Aby uzyskać tyle zboża, należałoby obsiać kilkukrotnie całą kulę ziemską i zebrać plon. Okazało się, że władca nie zawsze może godnie nagrodzić swego nadwornego geniusza.
Już starożytni Grecy postrzegali muzykę jako sztukę matematyczną. Wiele jest w niej tajemniczych symboli, żelaznych reguł i liczb określających częstotliwości, tempo, takty, akordy i interwały. Ten niewątpliwy choć tajemniczy związek między muzyką a matematyką nasuwa pytanie, czy matematyczny umysł pomaga w tworzeniu doskonałej muzyki i czy wyobraźnia matematyczna i muzyczna mają wspólne korzenie. Podobno badania naukowe potwierdziły, że słuchanie muzyki Mozarta poprawia koncentrację, pobudza logiczne myślenie i pozytywnie wpływa na skuteczność uczenia się (nazwano to nawet efektem Mozarta), choć być może podobny skutek odnosi też muzyka Bacha czy Beethovena. Bezsprzecznie stwierdzono, że nauka śpiewu i fortepianu daje lepsze skutki w rozwijaniu abstrakcyjnego rozumowania niż np. nauka programowania. Być może w szkołach zamiast wprowadzania coraz większej liczby zajęć komputerowych warto powrócić do powszechnego kształcenia muzycznego (czytanie nut i umiejętność gry na instrumencie już dawno wypadły z podstawy programowej).
Muzyki Mozarta zachwyca swoją doskonałością już od 260 lat. Stała się w muzyce klasycznej kanonem piękna. Podobną rolę w sztuce wizualnej stanowi od czasów starożytnych złota proporcja. Zbadajmy zatem, czy przypadkiem nie kryje się ona w niezwykłej, a jednocześnie bardzo naturalnej dla ludzkiego ucha harmonii utworów Mozarta.
Złotym nazywamy taki podział odcinka na dwie części, że stosunek całości do dłuższej części jest równy stosunkowi dłuższej części do krótszej.
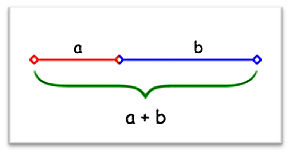
Zapisując to w postaci równania, otrzymamy [tex]\frac{a+b}{b}=\frac{b}{a}[/tex]. Stosunek ten zwyczajowo oznacza się grecką literą φ. Podstawiając ją do powyższej zależności otrzymujemy 1/φ + 1 = φ, czyli φ2– φ – 1 = 0.
Dodatnim pierwiastkiem tego równania jest liczba złota φ =[tex]\frac{\sqrt{5}+1}{2}[/tex]≈ 1,618...
Przyjrzyjmy się teraz sonatom Mozarta. Napisał ich w różnych okresach życia około 90 (na skrzypce, pianino, klawesyn, wiolonczelę i zestawy kilku instrumentów, w tym 28 solowych na pianino). Ich spis można znaleźć w tzw. Katalogu Köchla, zestawionym chronologicznie i tematycznie rejestrze wszystkich dział Mozarta opracowanym w 1862 roku przez Ludwiga von Köchla i opublikowanym pod nazwą Chronologisch-thematisches Verzeichnis sämtlicher Tonwerke Wolfgang Amadé Mozarts (w skrócie KV – Köchel Verzeichnis).
Poszukiwaniem złotego podziału w mozartowskich sonatach na pianino zajmował się amerykański matematyk z Alma College - John Putz. W czasach Mozarta sonata przybrała wyraźną trójdzielną formę. Pierwsza część nazywana ekspozycją wprowadzała dwa kontrastujące tematy - pierwszy w tonacji głównej, żywy i dynamiczny oraz drugi – w tonacji pokrewnej, bardziej stonowany i melancholijny. Część druga zwana przetworzeniem była swobodną interpretacją tematów pod względem melodycznym, rytmicznym, harmonicznym i fakturalnym. Ostatnia część zwana repryzą lub reekspozycją stanowiła zakończenie sonaty, w którym powracały tematy główne. Powstaje naturalne pytanie, czy Mozart zastosował w swoich sonatach złoty podział, traktując ekspozycję jako krótszy, a przetworzenie i repryzę jako dłuższy odcinek utworu. Za miarą długości danego odcinka przyjmujemy liczbę tworzących go taktów.
W poniższej tabeli zebrano sonaty solowe na pianino Mozarta, podając liczbę taktów ekspozycji oraz przetworzenia z repryzą, całkowitą liczbę taktów sonaty i stosunki całości do dłuższej części utworu oraz dłuższej części do krótszej.
| KV | ekspozycja a |
przetworzenie+repryza b |
całość a+b |
a+b/b | b/a |
| 279 I | 38 | 62 | 100 | 1,6129 | 1,6316 |
| 279 II | 28 | 46 | 74 | 1,6087 | 1,6429 |
| 279 III | 56 | 102 | 158 | 1,5490 | 1,8214 |
| 280 I | 56 | 88 | 144 | 1,6364 | 1,5714 |
| 280 II | 24 | 36 | 60 | 1,6667 | 1,5000 |
| 280 III | 77 | 113 | 190 | 1,6814 | 1,4675 |
| 281 I | 40 | 69 | 109 | 1,5797 | 1,7250 |
| 281 II | 46 | 60 | 106 | 1,7667 | 1,3043 |
| 282 I | 15 | 18 | 33 | 1,8333 | 1,2000 |
| 282 II | 39 | 63 | 102 | 1,6190 | 1,6154 |
| 283 I | 53 | 67 | 120 | 1,7910 | 1,2642 |
| 283 II | 14 | 23 | 37 | 1,6087 | 1,6429 |
| 283 III | 102 | 171 | 273 | 1,5965 | 1,6765 |
| 284 I | 51 | 76 | 127 | 1,6711 | 1,4902 |
| 309 I | 58 | 97 | 155 | 1,5979 | 1,6724 |
| 310 I | 49 | 84 | 112 | 1,5342 | 1,8718 |
| 311 I | 39 | 73 | 133 | 1,5833 | 1,7143 |
| 330 I | 58 | 92 | 150 | 1,6304 | 1,5862 |
| 330 II | 68 | 103 | 171 | 1,6602 | 1,5147 |
| 332 I | 93 | 136 | 229 | 1,6838 | 1,4624 |
| 332 II | 90 | 155 | 245 | 1,5806 | 1,7222 |
| 333 I | 63 | 102 | 165 | 1,6176 | 1,6190 |
| 333 II | 31 | 50 | 81 | 1,6200 | 1,6129 |
| 457 I | 74 | 93 | 167 | 1,7957 | 1,2568 |
| 533 I | 102 | 137 | 239 | 1,7445 | 1,3431 |
| 533 II | 46 | 76 | 122 | 1,6053 | 1,6522 |
| 545 I | 28 | 45 | 73 | 1,6222 | 1,6071 |
| 547 I | 78 | 118 | 196 | 1,6610 | 1,5128 |
Oczywiście podane ilorazy dają tylko wymierne przybliżenia liczby złotej, gdyż liczby taktów są naturalne, ale i tak otrzymane wyniki robią niesamowite wrażenie. Na szczególną uwagę zasługuje tu Sonata nr 1 C-dur KV 279 I (pierwsza w katalogu), w której złoty podział jest wręcz doskonały. W 100-taktowym utworze podział w stosunku 62:38 realizuje złotą proporcję najlepiej ze wszystkich innych możliwych podziałów na odcinki o długości naturalnej. O przypadkowości nie może tu więc być mowy.
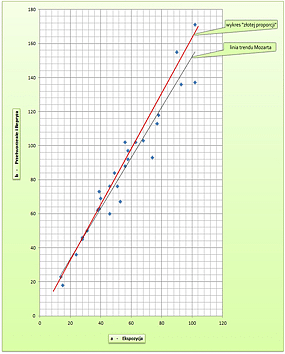
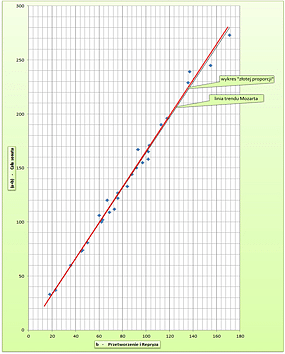
Dla lepszego zobrazowania odkrytej zależności zaznaczmy otrzymane dane w układzie współrzędnych. Na pierwszym diagramie każdy utwór jest reprezentowany przez punkt o współrzędnych (a, b). Na wykresie kolorem czarnym zaznaczono też prostą regresji liniowej (czyli prostą najlepiej dopasowaną do zestawu danych) oraz kolorem czerwonym funkcję liniową, której współczynnik kierunkowy jest dokładnie równy złotej liczbie. Drugi diagram przedstawia analogiczne dane dla współrzędnych (b, a+b). Tu widoczna zgodność jest jeszcze większa. Rzeczywiście współczynnik korelacji linii regresji z danymi wynosi 0.99, czyli jest bardzo wysoki (gdyby wszystkie punkty leżały dokładnie na tej linii, wynosiłby 1).
Oba diagramy nie pozostawiają wątpliwości, że nawet jeśli w kompozycji Mozart nie kierował się ściśle rachunkami, to przynajmniej intuicyjnie dążył do uzyskania złotego podziału.
Innym matematycznym elementem muzyki Mozarta są występujące w nich symetrie własne zauważalne podobnie jak w parkietażach płaszczyzny lub symetriach wzorów fryzowych. Mamy podstawowy temat muzyczny pełniący rolę ornamentu. Ta melodia powtarza się potem w różnych układach geometrycznych (jest odbita względem osi pionowej lub poziomej, odbita środkowosymetrycznie, czyli obrócona o 180° albo odbita w osi poziomej i przesunięta, tworząc symetrię z poślizgiem). Czasem w kolejnych powtórzeniach głównego tematu zmienia się wysokość pojedynczej nuty lub kilku nut. W muzyce nazywa się to transpozycją, a w matematyce - translacją. W ten sposób tworzy się regularna, powtarzalna cyklicznie kompozycja mozaikowa. Można ją dokładnie analizować, obserwując zapis nutowy partytury. Tego typu zabawy z symetrią odnajdujemy także w utworach Bacha (np. w Crab Canon), a u Mozarta geometryczne symetrie doskonale słychać np. w Symfonii nr 40.
Oczywiście gdyby w muzyce stosować tylko symetrie, byłaby zbyt nudna. Lubimy pewną przewidywalność utworu, ale też chcemy być zaskakiwani. Zbytnia powtarzalność nudzi, ale ciągłe zaskakiwanie też jest męczące. Mozart dozował muzyczne symetrie z doskonałym wyczuciem. Słuchając jego muzyki, jesteśmy przygotowani na kolejny temat, ale wiemy też, że nas czymś nowym zaskoczy.
Niezwykle interesująca z matematycznego punktu widzenia jest także kompozycja Mozarta Musical Dice Game Minuet, czyli Muzyczna gra w kości, napisana w 1787 roku. Jest to 16-taktowy menuet wraz z instrukcją, jak należy go grać. Menuet składa się z 12 części. Najpierw grana jest pierwsza część, a kolejna wybierana jest za pomocą rzutu dwoma kostkami do gry (wyniki uzyskane na kostkach są sumowane). Mozart tak skomponował ten utwór, że każda część pasuje do poprzedniej i następnej niezależnie od ich kolejności. W bardziej rozbudowanym eksperymencie można nawet zmieniać kolejność taktów w poszczególnych częściach. Daje to biliardy różnych możliwości wykonania tego utworu (a także ciekawe zadania z kombinatoryki).
Bibliografia:
- John Putz, The Golden Section and the Piano Sonatas of Mozart, Mathematics Magazine, vol. 68, No 4, 1995.
- Paul Barz, Mozart. Książę i Papageno, Vizja Press & IT, Warszawa 2006.
- Mario Livio, The Mathematics of Mozart's Music, audycja w National Public Radio 2006.
- Roy Howat, Debussy in proportion. A Musical Ananlysis, Cambridge Univerity Press 1983.






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 


Bardzo ciekawa analiza, ale
Bardzo ciekawa analiza, ale Mozart nie mógł komponować utworów przeznaczonych na pianino. Pianino to późniejszy instrument - odmiana fortepianu. Zresztą fortepian w czasach Mozarta był mało popularny. Koncertowym instrumentem klawiszowym był wówczas klawesyn, a w domu klawikord albo ich różne odmiany.