| więcej informacji o tekście: |
 Cóż ciekawego dla matematyka można zobaczyć na wakacjach? Na przykład kolonię domków kempingowych na łące pod lasem. Przyjrzyjmy się im dokładniej.
Cóż ciekawego dla matematyka można zobaczyć na wakacjach? Na przykład kolonię domków kempingowych na łące pod lasem. Przyjrzyjmy się im dokładniej.
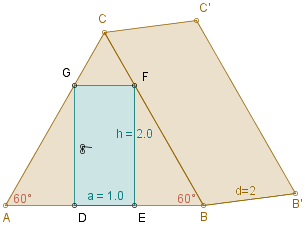 Toż to graniastosłupy prawidłowe o podstawach trójkątnych.
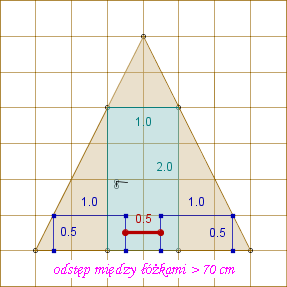
Bardzo oszczędnie zrobione, bo drzwi ledwie się mieszczą na ścianie frontowej. Wymiary domków są przedstawione na rysunku obok.
Toż to graniastosłupy prawidłowe o podstawach trójkątnych.
Bardzo oszczędnie zrobione, bo drzwi ledwie się mieszczą na ścianie frontowej. Wymiary domków są przedstawione na rysunku obok.
Domki mają z tyłu okna, ale zasłonięte, więc nie można zajrzeć do środka.Ciekawe, czy te domki są jedno-, czy dwuosobowe.
Problem A. Czy w takim domku kempingowym mieszą się dwa łóżka? (Typowe łóżko ma szerokość s = 90 cm i długość 2 m.)
Uczymy matematyki w szkole w taki sposób, że po takiej opowieści większość uczniów nie daje się nabrać i wie, że chodzi tu o kolejne zadanie o trójkącie. Wiedzą, że spodziewamy się rozumowania podobnego do poniższego.
Rozumowanie 1.
Trójkąt ADG jest połówką trójkąta równobocznego o wysokości DG, więc
2AD ./2 = h ,
skąd
AD = h /.
Zatem
AB = a + 2AD = a + 2h /= 1 + 4 /
.
Dalej za pomocą kalkulatora obliczamy:
AB1 + 4 / 1,73
3,30 > 2 . 0,90 = 1,8 ,
więc AB > 2s. W tym domku zmieszczą się dwa łóżka.
Jesteśmy skłonni zaakceptować takie rozwiązanie, choć zapewne bardziej ucieszy nas poniższe:
Rozumowanie 2.
Trójkąt ADG jest połówką trójkąta równobocznego o wysokości DG, więc
AD = AG / 2 .
Ponieważ przeciwprostokątna jest dłuższa od przyprostokątnych, więc
AG > h = 2 .
Zatem
AD = AG / 2 > h / 2 = 1 > 0,90 ,
więc w tym domku zmieszczą się dwa łóżka, co więcej odstęp między nimi jest większy od 1,2 m.
Kłopotliwe pytanie 1.
Dlaczego na matematyce śpimy na cienkich materacach, a nie na prawdziwych łóżkach?
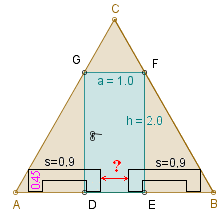
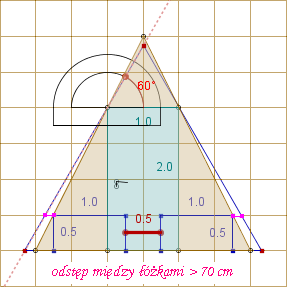
Problem B. Czy w takim domku kempingowym mieszą się dwa łóżka? (Typowe łóżko ma szerokość s = 90 cm, długość 2 m i wysokość w = 45 cm.)
Sprytne Rozumowanie 2. nie jest już teraz wystarczające. Za wzorowe jesteśmy skłonni uznać poniższe:
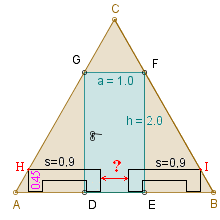
Rozumowanie 3.
Trójkąt GFC ma wysokość równą a ./2,
więc trójkąt HIC ma wysokość równą
h - w + a ./2 .
Stąd bok HI trójkąta HIC ma długość
( h - w + a ./2 ) . 2/
.
Dalej za pomocą kalkulatora obliczamy:
HI = (2 - 0,45 + 1 ./2) . 2/

2,78978583 > 2 . 0,90 = 1,8 ,
więc w tym domku zmieszczą się dwa łóżka.
Kłopotliwe pytanie 2.
W ten sposób uczymy przyszłego stolarza, mechanika, inżyniera, ekonomistę. Co oni sobie o nas myślą? Co ważniejsze, co oni sobie myślą o matematyce?




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
