Na skróty - z niespodziankami

Niech dany będzie kąt prosty o wierzchołku O i punkt C, leżący w obszarze tego kąta, odległy o p i q od ramion kąta. Niech A, B oznaczają punkty przecięcia prostej przechodzącej przez C z ramionami tego kąta.

Tak może się zaczynać wiele zadań. Omówimy tu dokładniej kilka problemów, nieco zbliżonych do rzeczywistości, w których obszar kąta utożsamimy z trawnikiem.

ZADANIE 1.   Jak poprowadzić (prostą) drogę AB przez C, by odciąć z trawnika jak najmniejszy obszar (trójkąt)?

ZADANIE 2.   Jak poprowadzić (prostą) drogę AB przez C, by odciąć jak najmniejszy fragment żywopłotu rosnącego wzdłuż ramion kąta ?

ZADANIE 3.   Jak wybrać (prostą) trasę AB przez C, by zadeptać jak najmniej trawnika , (AB jest najmniejsze)?

Odpowiedzi można udzielać na wiele sposobów. Droga AB przez C jest określona jednoznacznie przez każdą z wielkości: AO, BO, x=AC_A, y=BC_B, BO / AO = tg .
My będziemy podawać wielkości x₀, y₀ opisujące optymalną linię A₀B₀.

ZADANIE 1.   Jak poprowadzić (prostą) drogę AB przez C, by odciąć z trawnika jak najmniejszy obszar (trójkąt)?

Uzasadnienie
Gdy x₀ = p, to y₀ = q i A₀C = B₀C (dlaczego?). Wtedy różnica pól trójkątów ABO, A₀B₀O jest równa polu czerwonego trójkąta (wskaż pary trójkątów przystających). Zatem jest nieujemna.

Uwaga 1
Dla innych trawników odpowiedź i uzasadnienie są identyczne (przesuwając K, zmienisz kąt ).

ZADANIE 2.   Jak poprowadzić (prostą) drogę AB przez C, by odciąć jak najmniejszy fragment żywopłotu rosnącego wzdłuż ramion kąta ?

Uzasadnienie
Gdy x₀ = p^1/2q^1/2, to y₀ = p^1/2q^1/2   (bo trójkąty A₀C_AC, CC_BB₀ są podobne).
Różnica (AO + OB) - (A₀O + OB₀) jest równa:
   BB₀ - AA₀  w przypadku 1, gdy A leży na odcinku A₀C_A ,
   AA₀ - BB₀  w przypadku 2, gdy A leży poza odcinkiem A₀C_A.
Przypadek 1.
Z podobieństwa trójkątów AC_AC i CC_BB mamy:

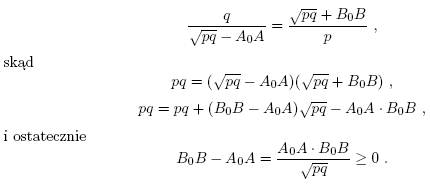
Przypadek 2. Uzasadnienie jest niemal identyczne - dlatego pomijamy tu szczegóły.

Uwaga 2
Dla innych trawników odpowiedź i uzasadnienie są identyczne (przesuwając K, zmienisz kąt ).

Uwaga 3
Odcinki o długości x₀ = y₀ = p^1/2q^1/2 można skonstruować cyrklem i linijką.
Jest to klasyczna konstrukcja opisana w wielu podręcznikach.

ZADANIE 3.   Jak wybrać (prostą) trasę AB przez C, by zadeptać jak najmniej trawnika , (kiedy długość AB jest najmniejsza)?

Uzasadnienie
Gdy x₀ = p^1/3q^2/3, to y₀ = p^2/3q^1/3   (bo trójkąty A₀C_AC, CC_BB₀ są podobne)
oraz   tg = (q/p)^1/3   (sprawdź).

Zatem wartość najmniejsza f jest przyjmowana dla kąta = .

Niespodzianka 1
Gdy p = 1 i q = 2, to x₀ = 2^1/3 .
Od niemal 200 lat wiadomo, że odcinka długości 2^1/3 nie można skonstruować cyrklem i linijką. Zatem, w przeciwieństwie do poprzednich zadań, to zadanie nie ma zgrabnego rozwiązania geometrycznego. Zaskakujące?

W porównaniu z poprzednimi, następujące zadanie brzmi jeszcze bardziej realistycznie:

ZADANIE 4.   Trasa biegnie wzdłuż ramion trawnika . Jak wytyczyć (prostą) ulicę AB przez C, by skrócić tę trasę maksymalnie?

Nie będziemy tu podawać szczegółów rozumowania (są dość żmudne).
Czerwony wykres funkcji  f (x) = AO + OB - AB  pokazuje, jak duży jest skrót, ile zaoszczędzimy (idąc przez AB) w zależności od x (= AC_A). Z wykresu można odczytać odpowiedź - przesuń A tak, by osiągnąć największą wartość funkcji.

Niespodzianka 2
Widać, że czasami - przy pewnych wielkościach p i q (przesuwaj C), wykres stale opada. Funkcja nie ma największej wartości (dla x=0 funkcja nie jest określona).
Czasami wykres stale się podnosi, więc i wtedy funkcja nie ma największej wartości.
W takich przypadkach zadanie nie ma rozwiązania, nie ma największego skrótu. Zaskakujące?

Niespodzianka 3
Gdy   1/2 < q / p < 2   największy skrót jest dla

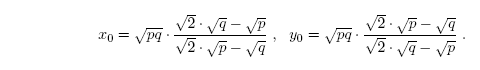
(Uzasadnienie jest dość żmudne.)
Zaskakujące jest jednak to, że w takich przypadkach optymalne rozwiązanie jest konstruowalne (można - żmudnie - cyrklem i linijką skonstruować odcinki x₀, y₀).
Pokazuje to, że zadanie 3 było wyjątkowe.
Zadziwiające?