Kwakoł jest (sumą) figurą zbudowaną z kół tak, jak pokazują poniższe przykłady.
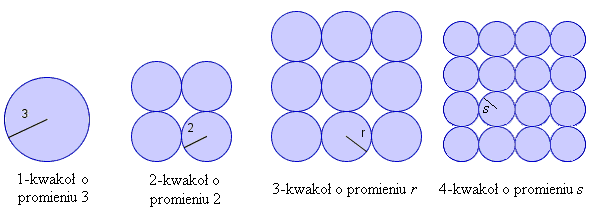
Zatem 3-kwakoł o promieniu 5 składa się z 9 kół i ma pole równe 225
. Będziemy mówili, że ma on dwie przekątne o długości
10 + 20
.
Zadanie A. Największy n-kwakoł zawarty w trójkącie równoramiennym, prostokątnym, o przyprostokątnej 3, styczny n kołami do przeciwprostokątnej, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie B. Największy n-kwakoł zawarty w trójkącie równoramiennym, prostokątnym, o przyprostokątnej 3, o przekątnej zawartej w osi symetrii trójkąta, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie C. Największy n-kwakoł zawarty w trójkącie równobocznym o boku 3, o przekątnej zawartej w osi symetrii trójkąta, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie D. Największy n-kwakoł zawarty w trójkącie równobocznym o boku 3, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie E. Największy n-kwakoł zawarty w trójkącie o bokach 5, 5, 8, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie F. Największy n-kwakoł zawarty w trójkącie o bokach 5, 5, 6, o przekątnej zawartej w osi symetrii trójkąta, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie G. Największy n-kwakoł zawarty w półkolu średnicy 2R, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie H. Największy n-kwakoł zawarty w półkolu średnicy 2R, o przekątnej zawartej w osi symetrii półkola, ma promień:
2) r = . . . . . . . . . . , gdy n = 2,
3) r = . . . . . . . . . . , gdy n = 3,
4) r = . . . . . . . . . . , gdy n = 4,
n) r = . . . . . . . . . . , gdy n = n (dla dowolnego n>1).
Zadanie I. Dla dużych wartości n, największy n-kwakoł zawarty w kwadracie o boku a ma pole równe w przybliżeniu . . . . . . . . . . .
Zadanie J. Dla dużych wartości n, największy n-kwakoł zawarty w kole o promieniu R, ma pole równe w przybliżeniu . . . . . . . . . ..
Zadanie K. Dla dużych wartości n, największy n-kwakoł zawarty w trójkącie równobocznym o boku a, ma pole równe w przybliżeniu . . . . . . . . . . .
