| więcej informacji o tekście: |
Naszkicuj w 20 sekund wykres funkcji
 Większość z nas, przyzwyczajona jest do zadań - pułapek,
nie da się nabrać
i zauważy problem dziedziny tej funkcji.
Większość z nas, przyzwyczajona jest do zadań - pułapek,
nie da się nabrać
i zauważy problem dziedziny tej funkcji.
(Porównaj z tekstem 'Przychodzi funkcja do lekarza'.)
Oczywiście x2-1 nie może być mniejsze od 0,
czyli liczby z przedziału (-1,1) nie należą do dziedziny.
Wzór funkcji f kojarzy nam się z funkcją $y = \sqrt{x}$ i wielu ... daje się na to nabrać.
Tak naprawdę funkcja f wygląda następująco (przy różnych zakresach na osiach):
Można to też zobaczyć rachunkowo:
$\color{blue}\sqrt{x^2-1} = \sqrt{x^2\cdot \left(1-\frac{1}{x^2}\right)} = |x|\cdot\sqrt{1-\frac{1}{x^2}} .$
W ostatnim wyrażeniu dla dużych x pod pierwiastkiem jest prawie 1. Możemy więc zapisać:
$\color{blue} f(x)=\sqrt{x^2-1} \approx |x|\cdot\sqrt{1} =|x| $ dla dużych x .
Podobnie można zapisać dla funkcji $\color{green} g(x) = \sqrt{x^2-17}$ :
$\color{green} \sqrt{x^2-17} = \sqrt{x^2\cdot \left(1-\frac{17}{x^2}\right)} = |x|\cdot\sqrt{1-\frac{17}{x^2}} .$
W ostatnim wyrażeniu dla dużych x pod pierwiastkiem jest prawie 1. Możemy więc zapisać:
$\color{green} g(x)=\sqrt{x^2-17} \approx |x|\cdot\sqrt{1} =|x| $ dla dużych x .
Podobnie można zapisać dla funkcji $\color{red} h(x) = \sqrt{x^2-x}$ :
$\color{red}\sqrt{x^2-x}=\sqrt{x^2\cdot\left(1-\frac{1}{x}\right)}=|x|\cdot\sqrt{1-\frac{1}{x}}.$
W ostatnim wyrażeniu dla dużych x pod pierwiastkiem jest prawie 1. Możemy więc zapisać:
$\color{red} h(x)=\sqrt{x^2-x} \approx |x|\cdot\sqrt{1} = |x| $ dla dużych x .
Wydaje się, że wszystkie te funkcje wyglądają prawie tak, jak wartość bezwględna y = | x | .
Jednak nie całkiem jest to prawdą!!!
Nie ma błędu w powyższych rachunkach,
jednak przybliżenia trzeba 'ostrożnie' interpretować.
Wężyk $\approx$ bywa zdradliwy!
Oblicz na kalkulatorze.
| x | ||||
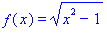 | 11,95826074 | 121,99590157 | 1221,99959083 | 12221,99995909 |
| x | ||||
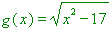 | 11,26942767 | 121,93030796 | 1221,99304417 | 12221,99930453 |
| x | ||||
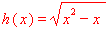 | 11,48912529 | 121,49897119 | 1221,49989767 | 12221,49998977 |
Dla f i g faktycznie widać, że bardzo mało różnią się od funkcji
y = |x|.
Jednak dla h już tak nie jest. Liczby nie kłamią!
Sprawdź jak jest dla innych argumentów, również ujemnych.
Widać, że $h(x) \approx |x-\frac{1}{2}|$ .
Spróbuj odgadnąć jak się zachowują poniższe funkcje (dla dużych x):
Możesz użyć poniższego 'kalkulatora'.
| x | ||||
| 8,48528137 | 118,96217886 | 1218,99630844 | 12218,99963172 |
Jak już mamy hipotezy, to można je zweryfikować rachunkiem podobnym do poniższego bazującym na wzorach skróconego mnożenia. Sprawdź, że zachodzą poszczególne równości i nierówności (dla dużych x):
$|x+\frac{5}{2}|-\sqrt{x^2+5x}= \sqrt{(x+\frac{5}{2})^2}-\sqrt{x^2+5x} = \frac{(x+\frac{5}{2})^2-(x^2+5x)}{\sqrt{(x+\frac{5}{2})^2}+\sqrt{x^2+5x}} \leq \frac{\frac{25}{4}}{|x+\frac{5}{2}|} \leq \frac{25}{4x} .$
To oznacza, że dla coraz większych x różnica między funkcjami $y=|x+\frac{5}{2}|$ i $y=\sqrt{x^2+5x}$ jest coraz mniejsza.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
