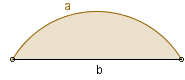Na rysunku widać odcinek koła, to znaczy jeden z dwóch obszarów ograniczonych okręgiem i cięciwą tego okręgu. Będziemy rozważać tylko mniejszy z tych dwóch obszarów, czyli taki, że środek koła nie leży w jego wnętrzu. W artykule Odcinek koła (1) wyznaczyliśmy geometrycznie (i
elementarnie) PRZYBLIŻONE wzory na pole odcinka koła, w zależności od długości: a - łuku i b - cięciwy.
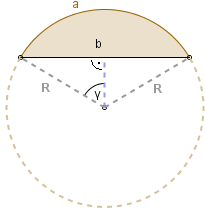Nietrudno podać DOKŁADNY wzór na pole P odcinka koła, w zależności od promienia R okręgu i kąta
mierzonego w radianach (patrz rysunek):
czyli
Wielkości a i b też można wyznaczyć w zależności od R i :
Uwaga 1
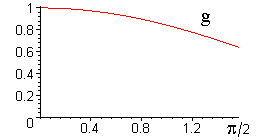
Powyższe obserwacje wystarczą do zbadania błędu względnego wzoru PRZYBLIŻONEGO P1 na pole odcinka koła (wyprowadzenie wzoru jest tutaj):
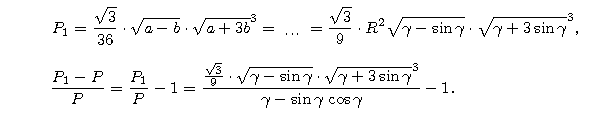
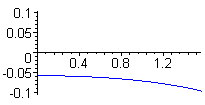
Z wykresu powyższej funkcji dla
z przedziału (0, 
/2]
odczytujemy, że wartości błędu względnego mieszczą się w przedziale [-0,1 , 0,1], czyli że jest on mniejszy niż 10-procentowy.
Tak samo można zbadać PRZYBLIŻONE wzory P2 i P3 (omówione tutaj).
w zależności od wielkości a i b?
Wystarczyłoby z zależności
wyznaczyć R i
, a potem wstawić do wzoru
Widać, że kłopot polega na wyznaczeniu takiego , że
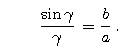
Niech g oznacza funkcję opisaną wzorem
i niech f oznacza funkcję odwrotną do g.
Wtedy
Przy takich oznaczeniach
.
Byłby to poszukiwany wzór, gdyby tylko znaleźć jeszcze wzór na f.
Ale takiego wzoru nie ma, tzn. nie ma wzoru na wyliczone z równania
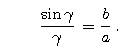
Jesteśmy więc skazani na przybliżenia.
Uwzględniając, że
,
dostajemy przybliżone równanie
,
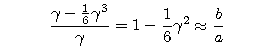skąd
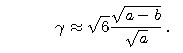
Stąd otrzymujemy kolejny wzór PRZYBLIŻONY
.
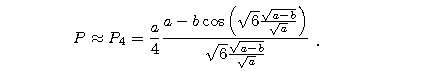Gdy uwzględnimy, że
,
to poprzednia postać przybliżenia zamieni się na bardziej znośny wzór:
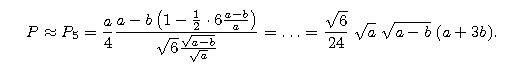
Dokładność tego ostatniego wzoru nie jest zbyt duża. Błąd względny nie przekracza 12,5%.
Gdy jednak uwzględnimy, że
, to przybliżenie
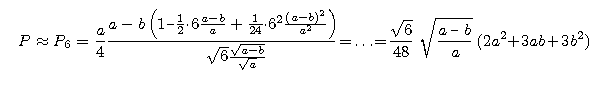
ma błąd względny nie większy od 1,2%.
Ciąg (xn) jest zbieżny do (pewnego) rozwiązania równania h(x) = 0.
Zastosujmy ten sposób dla funkcji
, której dodatnie miejsce zerowe jest rozwiązaniem równania
(sprawdź).
Ciąg przybliżeń otrzymamy z powyższego pomysłu Newtona:
.
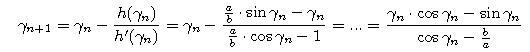Zaczynając od
1=
/2, dostajemy kolejno:
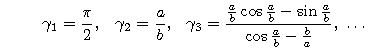
Uwzględniając te wartości we wzorze na pole
,
dostaniemy ciąg kolejnych przybliżeń:
.
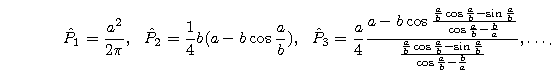
Wzory te są coraz bardziej koszmarne.
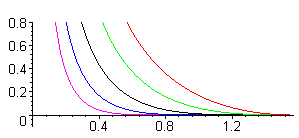
Przy USTALONYCH wartościach a, b ciąg ten daje coraz lepsze przybliżenia wartości pola odcinka koła, jednak nie ma NIEZALEŻNEGO od a, b oszacowania tempa tej zbieżności. Na rysunku obok widać błędy względne początkowych pięciu wzorów. Dla każdego wzoru są takie wartości a, b (o ilorazie a/b bliskim 1), że błąd względny jest duży, co najmniej 50%.
Zatem wzory te są nie tylko koszmarne, ale i marne.
Powyższe rozważania można uznać za raport z fiaska odniesionego w poszukiwaniach dokładnego wzoru. Doświadczenie podpowiada, że takiego wzoru nie ma. Ale jak to: nie ma? Zbiory szkolnych zadań wypaczają ogląd matematyki w tym sensie, że sugerują, iż odpowiada ona na każde postawione pytanie, podczas gdy w rzeczywistości opisuje ona tylko bardzo mały skrawek swojego pola badań. To zachwycające, że mimo to jest tak skuteczna w zastosowaniach w innych dziedzinach wiedzy.
Wzoru (pewnie) nie ma. Może się jednak zdarzyć, że za jakiś czas pojawi się. Gdy ludzie dostatecznie często będą natykać się na problem wyznaczenia
z zależności 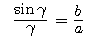, to uznają, że należy NAZWAĆ jakoś występująca w nim funkcję f, stablicować jej wartości, zaszyć w kalkulatorach ich przybliżenia i może nawet uczyć o niej w szkole. Wtedy uznamy, że istnieje ów poszukiwany wzór.
Powyższy tekst powstał po przeczytaniu artykułu Marka Kordosa 'Rozprawka o metodzie', Delta 7 (2015). Gorąco polecamy jego lekturę.
